Appearance
《数据结构与算法 JavaScript 描述》记录
前言
曾经的我一度认为,没必要去学习数据结构和算法,因为没用数据结构和算法,我一样可以很好的完成我的工作。但随着自己的成长,越发觉得算法和数据结构是多么的重要!
为什么推荐这本书
市面上的算法书有很多,厚的像《算法-第四版》、薄一点像是《算法图解》、《啊哈!算法》我都有买,但是读到一半都卡壳了。原因有:
- 代码不是基于 JavaScript,看其他语言的代码虽然大致看得懂,但还是有一定的成本。
- 本书会先完整的介绍了一遍数据结构,再开始搞算法,这个比较适合我。
- 本书只有 200 多页,其中前两章是介绍 JS 的一些 API,所以读起来非常的轻松。
列表(List)
:::demo
vue
<template>
<div class="demo">
<iframe
src="//player.bilibili.com/player.html?aid=253369241&bvid=BV1yY411b7US&cid=487271372&page=1"
scrolling="no"
border="0"
frameborder="no"
framespacing="0"
allowfullscreen="true"
>
</iframe>
</div>
</template>
<style>
.demo > iframe {
width: 100%;
height: 450px;
}
</style><template>
<div class="demo">
<iframe
src="//player.bilibili.com/player.html?aid=253369241&bvid=BV1yY411b7US&cid=487271372&page=1"
scrolling="no"
border="0"
frameborder="no"
framespacing="0"
allowfullscreen="true"
>
</iframe>
</div>
</template>
<style>
.demo > iframe {
width: 100%;
height: 450px;
}
</style>:::
大学时我是有上《数据结构》这门课的,但是好像没听过 列表 这一个数据结构。
列表是一组有序的数据。每个列表中的数据项称为元素。在 JavaScript 中,列表中的元素 可以是任意数据类型。列表中可以保存多少元素并没有事先限定,实际使用时元素的数量 受到程序内存的限制。
列表具有以下的 API:
| 属性/方法 | 含义 |
|---|---|
| listSize(属性) | 列表的元素个数 |
| pos(属性) | 列表的当前位置 |
| length(属性) | 返回列表中元素的个数 |
| clear(方法) | 清空列表中的所有元素 |
| toString(方法) | 返回列表的字符串形式 |
| getElement(方法) | 返回当前位置的元素 |
| insert(方法) | 在现有元素后插入新元素 |
| append(方法) | 在列表的末尾添加新元素 |
| remove(方法) | 从列表中删除元素 |
| front(方法) | 将列表的当前位置设移动到第一个元素 |
| end(方法) | 将列表的当前位置移动到最后一个元素 |
| prev(方法) | 将当前位置后移一位 |
| next(方法) | 将当前位置前移一位 |
| currPos(方法) | 返回列表的当前位置 |
| moveTo(方法) | 将当前位置移动到指定位置 |
点击查看源码
测试代码
js
let names = new List<String>();
names.append("jimmy");
names.append("xuexue");
names.append("Jack");
names.append("Henry");
console.log(names.getElement()); // jimmy
names.next();
console.log(names.getElement()); // xuexue
names.clear();
names.append("Henry");
names.append("jimmy");
names.append("xuexue");
names.append("Jack");
names.moveTo(3);
console.log(names.getElement()); // jack
names.front();
console.log(names.getElement()); // henry
console.log(names.length); // 4let names = new List<String>();
names.append("jimmy");
names.append("xuexue");
names.append("Jack");
names.append("Henry");
console.log(names.getElement()); // jimmy
names.next();
console.log(names.getElement()); // xuexue
names.clear();
names.append("Henry");
names.append("jimmy");
names.append("xuexue");
names.append("Jack");
names.moveTo(3);
console.log(names.getElement()); // jack
names.front();
console.log(names.getElement()); // henry
console.log(names.length); // 4已经知道了列表的数据结构了,列表是一种最自然的数据组织方式,我的体验下来之后感觉好像和数组差不多的,不过封装了几个还蛮不错的方法。
列表具有以下的特点:
- 存储数据的顺序并不重要
- 不需要对数据进行查找
如果满足以上两个情况,列表就是最适合不过的数据结构了。
栈(Stack)
:::demo
vue
<template>
<div class="demo">
<iframe
src="//player.bilibili.com/player.html?aid=296290782&bvid=BV1aF411J7j7&cid=503512221&page=1"
scrolling="no"
border="0"
frameborder="no"
framespacing="0"
allowfullscreen="true"
>
</iframe>
</div>
</template>
<style>
.demo > iframe {
width: 100%;
height: 450px;
}
</style><template>
<div class="demo">
<iframe
src="//player.bilibili.com/player.html?aid=296290782&bvid=BV1aF411J7j7&cid=503512221&page=1"
scrolling="no"
border="0"
frameborder="no"
framespacing="0"
allowfullscreen="true"
>
</iframe>
</div>
</template>
<style>
.demo > iframe {
width: 100%;
height: 450px;
}
</style>:::
栈和列表是一种类似的数据结构,不过从上个例子也能看出来,列表是非常简陋的,几乎就是简单的处理数组的 API 相结合了,使用场景也相对有所限制。
栈则不同,栈再计算机世界有非常多的使用场景,比如 JS 执行时上下文其实就是个栈的结构。栈是一种高效的数据结构,因为数据只能在栈顶添加或删除,所以这样的操作很快,而且容易实现。
简单概括栈:
- 先进后出、后进先出
- 元素只能通过栈顶访问
栈具有以下 API:
| 属性/方法 | 含义 |
|---|---|
| push(方法) | 元素入栈 |
| pop(方法) | 元素出栈 |
| peek(方法) | 返回栈顶元素(不删除它) |
| clear(方法) | 清空栈内所有元素 |
| length(属性) | 记录栈内元素个数 |
| empty(属性) | 判断栈是否是空 |
实现代码
js
{
class Stack<T> {
dataStore: T[] = []
top: number = 0
constructor() {}
// 获取栈的长度
get length(): Number {
return this.dataStore.length
}
// 入栈方法
push(element: T): void {
this.dataStore.push(element)
this.top++
}
// 出栈方法
pop(): T {
// 数组的pop()方法就是删除数组的最后一个元素
if (this.dataStore.length !== 0) {
this.top--
// console.log("2222");
return this.dataStore.pop()
}
}
// 返回栈顶元素
peek(): T {
// console.log(111, this.dataStore, this.top);
return this.dataStore[this.top - 1]
}
// 清空栈
clear(): void {
this.top = 0
this.dataStore.length = 0
}
}
}{
class Stack<T> {
dataStore: T[] = []
top: number = 0
constructor() {}
// 获取栈的长度
get length(): Number {
return this.dataStore.length
}
// 入栈方法
push(element: T): void {
this.dataStore.push(element)
this.top++
}
// 出栈方法
pop(): T {
// 数组的pop()方法就是删除数组的最后一个元素
if (this.dataStore.length !== 0) {
this.top--
// console.log("2222");
return this.dataStore.pop()
}
}
// 返回栈顶元素
peek(): T {
// console.log(111, this.dataStore, this.top);
return this.dataStore[this.top - 1]
}
// 清空栈
clear(): void {
this.top = 0
this.dataStore.length = 0
}
}
}这里获取栈的长度使用了 getter,很多时候其实我并不知道 getter 和 setter的使用场景,但其实这个就是一个比较不错的使用场景,这里 length 是一个属性,我们当然也可以使用 length()方法来及逆行操作,但是就与整个语意不相符合。length更像是属性,如果是getLength才像是方法。
getter 和 setter 可以用来:
- 处理访问日志(getter)
- 类型检查(setter)
数制间的相互转换
可以利用栈将一个数字从一种数制转换成另一种数制。使用栈,在 JavaScript 中实现该算法就是小菜一碟。
js
function mulBase(num,base){
let s = new Stack()
do{
s.push(num%base)
num = Math.floor(num /= base)
}while(num>0)
let cinverted = ''
while(s.length>0){
converted += s.pop()
}
return converted
}
var newNum = mulBase(32, 2);
console.log('32转为2进制的结果为:'newNum)function mulBase(num,base){
let s = new Stack()
do{
s.push(num%base)
num = Math.floor(num /= base)
}while(num>0)
let cinverted = ''
while(s.length>0){
converted += s.pop()
}
return converted
}
var newNum = mulBase(32, 2);
console.log('32转为2进制的结果为:'newNum)判断一个数是否是回文数
类似于 dad、racecar 这种就是回文数,A man, a plan, a canal: Panama 和 1001 也是会问,而这种结构,使用栈也能够轻松的解决。
js
function isPalindrome(word) {
let s = new Stack()
for (let i = 0; i < word.length; i++) {
s.push(word[i])
}
let rword = ''
while (s.length > 0) {
rword += s.pop()
}
return word === rword
}
console.log(isPalindrome('hello'))
console.log(isPalindrome('racecar'))function isPalindrome(word) {
let s = new Stack()
for (let i = 0; i < word.length; i++) {
s.push(word[i])
}
let rword = ''
while (s.length > 0) {
rword += s.pop()
}
return word === rword
}
console.log(isPalindrome('hello'))
console.log(isPalindrome('racecar'))使用栈模拟递归
如 leetcode 中的爬楼梯问题、算阶乘问题,这种可以写成正常的写递归函数,也可以用栈的数据结构来实现。
如:计算阶乘
js
// 递归函数实现
function factorial(n) {
if (n === 0) {
return 1 // 0的阶乘为1
} else {
return n * factorial(n - 1)
}
}
// 栈实现
function fact(n) {
let s = new Stack()
while (n > 1) {
s.push(n--)
}
let product = 1
while (s.length > 0) {
product *= s.pop()
}
return product
}
console.log(factorial(5)) // 显示 120
console.log(fact(5)) // 显示 120// 递归函数实现
function factorial(n) {
if (n === 0) {
return 1 // 0的阶乘为1
} else {
return n * factorial(n - 1)
}
}
// 栈实现
function fact(n) {
let s = new Stack()
while (n > 1) {
s.push(n--)
}
let product = 1
while (s.length > 0) {
product *= s.pop()
}
return product
}
console.log(factorial(5)) // 显示 120
console.log(fact(5)) // 显示 120队列(Queue)
队列是一个更加复杂的列表,其只能在队尾插入元素,在队首删除元素。队列用于存储按顺序排列的数据,先进先出。队列的场景可以理解成是在食堂排队点餐的场景,只有队首的人点完了之后的人才能点餐,新来的人只能在队尾排队等候。
栈具有以下 API:
| 属性/方法 | 含义 |
|---|---|
| enqueue(方法) | 队尾添加元素 |
| dequeue(方法) | 队首删除元素 |
| front(方法) | 读取队首元素 |
| back(方法) | 读取队尾元素 |
| toString(方法) | 显示队列内的所有元素 |
| isEmpty(方法) | 判断队列是否为空 |
| clear(属性) | 清空队列 |
| length(属性) | 获取队列长度 |
js
{
class Queue<T> {
private dataStore: T[] = [];
get length(): number {
return this.dataStore.length;
}
enqueus(element: T) {
this.dataStore.push(element);
}
dequeus(): T | undefined {
return this.dataStore.shift();
}
front(): T {
return this.dataStore[0];
}
back(): T {
return this.dataStore[this.length - 1];
}
toString() {
return this.dataStore.map((item) => item).join("\n");
}
clear() {
this.dataStore.length = 0;
}
isEmpty() {
return this.length === 0;
}
}
}{
class Queue<T> {
private dataStore: T[] = [];
get length(): number {
return this.dataStore.length;
}
enqueus(element: T) {
this.dataStore.push(element);
}
dequeus(): T | undefined {
return this.dataStore.shift();
}
front(): T {
return this.dataStore[0];
}
back(): T {
return this.dataStore[this.length - 1];
}
toString() {
return this.dataStore.map((item) => item).join("\n");
}
clear() {
this.dataStore.length = 0;
}
isEmpty() {
return this.length === 0;
}
}
}基数排序(使用队列对数据进行排序)
对于 0~99 的数据,基数排序是将数据集合扫描两次,它不是最快的排序方法,但是是一种特别有意思的使用队列的排序算法。
例如现有数字:91, 46, 85, 15, 92, 35, 31, 22。经过基数排序,第一次扫描先从个位开始排序:
Bin 0:
Bin 1: 91, 31
Bin 2: 92, 22
Bin 3:
Bin 4:
Bin 5: 85, 15, 35
Bin 6: 46
Bin 7:
Bin 8:
Bin 9:Bin 0:
Bin 1: 91, 31
Bin 2: 92, 22
Bin 3:
Bin 4:
Bin 5: 85, 15, 35
Bin 6: 46
Bin 7:
Bin 8:
Bin 9:排序结果为:91, 31, 92, 22, 85, 15, 35, 46
再使用上回的结果,根据十位上的数字再次进行一次排序:
Bin 0:
Bin 1: 15
Bin 2: 22
Bin 3: 31, 35
Bin 4: 46
Bin 5:
Bin 6:
Bin 7:
Bin 8: 85
Bin 9: 91, 92Bin 0:
Bin 1: 15
Bin 2: 22
Bin 3: 31, 35
Bin 4: 46
Bin 5:
Bin 6:
Bin 7:
Bin 8: 85
Bin 9: 91, 92最后再取出数据,结果为:15, 22, 31, 35, 46, 85, 91, 92,我们发现已经排号序啦~
实现代码
js
let queues: Queue<Number>[] = [];
for (var i = 0; i < 10; ++i) {
queues[i] = new Queue<Number>(); // 数组的每一项都是队列
}
let nums = [];
for (var i = 0; i < 10; ++i) {
nums[i] = Math.floor(Math.floor(Math.random() * 101)); // 随机生成100以内10个数
}
console.log("BEFORE", nums);
const distribute = (
nums: number[],
queues: Queue<Number>[],
n: number,
digit: number
) => {
for (let i = 0; i < n; i++) {
if (digit == 1) {
// 个位排序
queues[nums[i] % 10].enqueus(nums[i]);
} else {
// 十位上的排序
queues[Math.floor(nums[i] / 10)].enqueus(nums[i]);
}
}
};
const collect = (queuss: Queue<Number>[], nums: number[]) => {
let i = 0;
for (let digit = 0; digit < 10; digit++) {
while (!queuss[digit].isEmpty()) {
nums[i++] = queuss[digit].dequeus() as number; // 根据队列出队再次排序赋值覆盖数组
}
}
};
// 第一次收集 -- 按个位进行排序
distribute(nums, queues, 10, 1);
collect(queues, nums);
// 第二次收集 -- 按十位进行排序
distribute(nums, queues, 10, 10);
collect(queues, nums);
console.log(nums)let queues: Queue<Number>[] = [];
for (var i = 0; i < 10; ++i) {
queues[i] = new Queue<Number>(); // 数组的每一项都是队列
}
let nums = [];
for (var i = 0; i < 10; ++i) {
nums[i] = Math.floor(Math.floor(Math.random() * 101)); // 随机生成100以内10个数
}
console.log("BEFORE", nums);
const distribute = (
nums: number[],
queues: Queue<Number>[],
n: number,
digit: number
) => {
for (let i = 0; i < n; i++) {
if (digit == 1) {
// 个位排序
queues[nums[i] % 10].enqueus(nums[i]);
} else {
// 十位上的排序
queues[Math.floor(nums[i] / 10)].enqueus(nums[i]);
}
}
};
const collect = (queuss: Queue<Number>[], nums: number[]) => {
let i = 0;
for (let digit = 0; digit < 10; digit++) {
while (!queuss[digit].isEmpty()) {
nums[i++] = queuss[digit].dequeus() as number; // 根据队列出队再次排序赋值覆盖数组
}
}
};
// 第一次收集 -- 按个位进行排序
distribute(nums, queues, 10, 1);
collect(queues, nums);
// 第二次收集 -- 按十位进行排序
distribute(nums, queues, 10, 10);
collect(queues, nums);
console.log(nums)优先队列
在一般情况下,从队列中删除的元素,一定是率先入队的元素。但是也有一些使用队列的应用,在删除元素时不必遵守先进先出的约定。这种应用,需要使用一个叫做优先队列的数据结构来进行模拟。
优先队列的现场场景也有很多,比如急诊科的候诊室,一般情况下都是正常的排队,
ts
interface Element {
data: any
code: number
}
class Queue {
private dataStore: Element[] = []
get length(): number {
return this.dataStore.length
}
enqueus(element: Element) {
this.dataStore.push(element)
}
dequeus(): any | undefined {
let priority = this.dataStore[0].code
let flag = false
for (let i = 1; i < this.dataStore.length; i++) {
if (this.dataStore[i].code < priority) {
flag = true
priority = i
}
}
return flag ? this.dataStore.splice(priority, 1)[0] : this.dataStore.shift()
}
front(): Element {
return this.dataStore[0]
}
back(): Element {
return this.dataStore[this.length - 1]
}
toString(): string {
return this.dataStore.map(item => item.data + '--' + item.code).join('\n')
}
clear(): void {
this.dataStore.length = 0
}
isEmpty(): boolean {
return this.length === 0
}
}interface Element {
data: any
code: number
}
class Queue {
private dataStore: Element[] = []
get length(): number {
return this.dataStore.length
}
enqueus(element: Element) {
this.dataStore.push(element)
}
dequeus(): any | undefined {
let priority = this.dataStore[0].code
let flag = false
for (let i = 1; i < this.dataStore.length; i++) {
if (this.dataStore[i].code < priority) {
flag = true
priority = i
}
}
return flag ? this.dataStore.splice(priority, 1)[0] : this.dataStore.shift()
}
front(): Element {
return this.dataStore[0]
}
back(): Element {
return this.dataStore[this.length - 1]
}
toString(): string {
return this.dataStore.map(item => item.data + '--' + item.code).join('\n')
}
clear(): void {
this.dataStore.length = 0
}
isEmpty(): boolean {
return this.length === 0
}
}以上的队列的方法几乎和普通队列基本是一样,区别在于我们需要定义队列中每个元素的数据类型,我们这里使用的 接口 来定义,每个元素有内容data和优先级code,每次出队会先根据队列中的优先级来进行出队.
测试代码
js
let que = new Queue()
/**
* 优先级一到5 1的最高 5最低
*/
que.enqueus({ data: '吃饭', code: 2 })
que.enqueus({ data: '睡觉', code: 2 })
que.enqueus({ data: '打豆豆', code: 2 })
que.enqueus({ data: '学习', code: 1 })
console.log(que.dequeus()) // { data: '学习', code: 1 }
console.log(que.dequeus()) // { data: '吃饭', code: 2 }
console.log(que.toString()) // 睡觉--2 \n 打豆豆--2let que = new Queue()
/**
* 优先级一到5 1的最高 5最低
*/
que.enqueus({ data: '吃饭', code: 2 })
que.enqueus({ data: '睡觉', code: 2 })
que.enqueus({ data: '打豆豆', code: 2 })
que.enqueus({ data: '学习', code: 1 })
console.log(que.dequeus()) // { data: '学习', code: 1 }
console.log(que.dequeus()) // { data: '吃饭', code: 2 }
console.log(que.toString()) // 睡觉--2 \n 打豆豆--2链表
在前面的例子中,我们所有的数据结构底层都是使用数组的完成的,诚然,数组是一个非常好用且非常易用的一个存储结构,但是数组并不总是组织数据的最佳结构。
数组的缺点
这是个经典的面试题,经常会问链表和数组的相比的优缺点。 在有的编程语言(C#、Java)数组的长度是固定,所以当数组长度满了以后想加入新的元素就会异常的困难,因为数组在内存中是顺序存储的,所以有时候删除和添加元素也是相对麻烦,会涉及其他元素向前或者向后移动。
链表的节点(Node)类型
JavaScript 可以基于对象实现链表,每个节点包含两个属性,分别是:
| 属性/方法 | 含义 |
|---|---|
| element | 保存节点上的数据 |
| next | 指向下一个节点的链接 |
ts
class Node {
constructor(public element: any = null, public next: Node | null = null) {}
}class Node {
constructor(public element: any = null, public next: Node | null = null) {}
}链表(LinkList)类型
栈具有以下 API:
| 属性/方法 | 含义 |
|---|---|
| head | 链表的头节点 |
| find | 查找给定的数据 |
| insert | 插入新节点 |
| remove | 删除节点 |
| display | 显示链表中的元素 |
ts
class LinkList<T> {
public head = new Node('head')
find(item: T): Node {
let currNode = this.head
while (currNode.next) {
if (currNode.element === item) {
break
} else {
currNode = currNode.next
}
}
return currNode
}
findPrevious(item: T): Node {
// 查找一个元素的前一个元素
let currNode = this.head
while (currNode.next) {
if (currNode.next.element === item) {
break
} else {
currNode = currNode.next
}
}
return currNode
}
insert(newElement: T, item: T): void {
let node = new Node(newElement)
let currNode = this.find(item)
node.next = currNode.next
currNode.next = node
}
remove(item: T): void {
let prevNode = this.findPrevious(item)
if (prevNode.next) {
prevNode.next = prevNode.next.next
}
}
display(): void {
let currNode = this.head
while (currNode) {
console.log(currNode.element)
if (currNode.next) {
currNode = currNode.next
} else {
break
}
}
}
}class LinkList<T> {
public head = new Node('head')
find(item: T): Node {
let currNode = this.head
while (currNode.next) {
if (currNode.element === item) {
break
} else {
currNode = currNode.next
}
}
return currNode
}
findPrevious(item: T): Node {
// 查找一个元素的前一个元素
let currNode = this.head
while (currNode.next) {
if (currNode.next.element === item) {
break
} else {
currNode = currNode.next
}
}
return currNode
}
insert(newElement: T, item: T): void {
let node = new Node(newElement)
let currNode = this.find(item)
node.next = currNode.next
currNode.next = node
}
remove(item: T): void {
let prevNode = this.findPrevious(item)
if (prevNode.next) {
prevNode.next = prevNode.next.next
}
}
display(): void {
let currNode = this.head
while (currNode) {
console.log(currNode.element)
if (currNode.next) {
currNode = currNode.next
} else {
break
}
}
}
}双向链表
尽管从链表的头节点遍历到尾节点很简单,但反过来,从后向前遍历则没那么简单。此时向链表插入一个节点需要更多的工作,我们需要指出该节点正确的前驱和后继。但是在从链表 中删除节点时,效率提高了,不需要再查找待删除节点的前驱节点了。
双向链表另外一个好处是因为每一个节点都有对应的前驱和后继,所以当我们获取某个节点时可以很方便的直到这个节点的前驱节点是什么,而这个是单向链表所比较难的,因为这个,所以我们也可以很方便的反向输出链表(只要找到最后一个节点,然后依次输出前一个节点即可)
ts
{
class Node {
constructor(
public element: any = null,
public previous: Node | null = null,
public next: Node | null = null
) {}
}
class LinkList<T> {
public head = new Node('head')
private find(item: T): Node {
let current = this.head
while (current.next) {
if (current.element === item) {
break
} else {
current = current.next
}
}
return current
}
private findPrevious(item: T): Node {
let current = this.head
while (current.next) {
if (current.next.element === item) {
break
} else {
current = current.next
}
}
return current
}
private findLast(): Node {
let curent = this.head
while (curent.next) {
curent = curent.next
}
return curent
}
public insert(element: T, item: T) {
let current = this.find(item)
let newNode = new Node(element)
if (current.next) {
// 双向链表插入元素
current.next.previous = newNode
newNode.next = current.next
newNode.previous = current
current.next = newNode
} else {
current.next = newNode
newNode.previous = current
}
}
public remove(item: T) {
let currNode = this.find(item)
if (!(currNode.next == null) && !(currNode.previous == null)) {
currNode.previous.next = currNode.next
currNode.next.previous = currNode.previous
currNode.next = null
currNode.previous = null
}
}
public display() {
let currNode = this.head
// console.log(currNode);
while (currNode) {
console.log(currNode.element, currNode.previous?.element)
if (currNode.next) {
currNode = currNode.next
} else {
break
}
}
}
public dispReverse(): void {
let last = this.findLast()
// console.log(last.element);
while (last) {
console.log(last.element)
if (last.previous) {
last = last.previous
} else {
break
}
}
}
}
// 测试代码
let doubleLink = new LinkList<string>()
doubleLink.insert('jimmy', 'head')
doubleLink.insert('xuexue', 'jimmy')
doubleLink.insert('henry', 'xuexue')
doubleLink.insert('jack', 'henry')
// doubleLink.remove("xuexue");
doubleLink.display()
console.log('*************************')
doubleLink.dispReverse()
}{
class Node {
constructor(
public element: any = null,
public previous: Node | null = null,
public next: Node | null = null
) {}
}
class LinkList<T> {
public head = new Node('head')
private find(item: T): Node {
let current = this.head
while (current.next) {
if (current.element === item) {
break
} else {
current = current.next
}
}
return current
}
private findPrevious(item: T): Node {
let current = this.head
while (current.next) {
if (current.next.element === item) {
break
} else {
current = current.next
}
}
return current
}
private findLast(): Node {
let curent = this.head
while (curent.next) {
curent = curent.next
}
return curent
}
public insert(element: T, item: T) {
let current = this.find(item)
let newNode = new Node(element)
if (current.next) {
// 双向链表插入元素
current.next.previous = newNode
newNode.next = current.next
newNode.previous = current
current.next = newNode
} else {
current.next = newNode
newNode.previous = current
}
}
public remove(item: T) {
let currNode = this.find(item)
if (!(currNode.next == null) && !(currNode.previous == null)) {
currNode.previous.next = currNode.next
currNode.next.previous = currNode.previous
currNode.next = null
currNode.previous = null
}
}
public display() {
let currNode = this.head
// console.log(currNode);
while (currNode) {
console.log(currNode.element, currNode.previous?.element)
if (currNode.next) {
currNode = currNode.next
} else {
break
}
}
}
public dispReverse(): void {
let last = this.findLast()
// console.log(last.element);
while (last) {
console.log(last.element)
if (last.previous) {
last = last.previous
} else {
break
}
}
}
}
// 测试代码
let doubleLink = new LinkList<string>()
doubleLink.insert('jimmy', 'head')
doubleLink.insert('xuexue', 'jimmy')
doubleLink.insert('henry', 'xuexue')
doubleLink.insert('jack', 'henry')
// doubleLink.remove("xuexue");
doubleLink.display()
console.log('*************************')
doubleLink.dispReverse()
}循环链表
循环链表和单链表是非常像的,都是一个节点只有一个后继,唯一区别的就在于最后一个节点的 next 指向的是 head 头节点,形成一个闭环。所以我们实现的代码其实只需要修改构造函数内部如:
ts
{
class Node {
constructor(public element: any = null, public next: Node | null = null) {}
}
class LinkList<T> {
public head = new Node('head')
constructor() {
this.head.next = this.head
}
find(item: T): Node {
let currNode = this.head
while (currNode.next && currNode.next.element !== 'head') {
if (currNode.element === item) {
break
} else {
currNode = currNode.next
}
}
return currNode
}
findPrevious(item: T): Node {
// 查找一个元素的前一个元素
let currNode = this.head
while (currNode.next) {
if (currNode.next.element === item) {
break
} else {
currNode = currNode.next
}
}
return currNode
}
insert(newElement: T, item: T): void {
let node = new Node(newElement)
let currNode = this.find(item)
node.next = currNode.next
currNode.next = node
}
remove(item: T): void {
let prevNode = this.findPrevious(item)
if (prevNode.next) {
prevNode.next = prevNode.next.next
}
}
display(): void {
let currNode = this.head
while (currNode.next) {
console.log(currNode.element)
if (currNode.next && currNode.next.element !== 'head') {
currNode = currNode.next
} else {
break
}
}
}
}
let list = new LinkList<string>()
list.insert('Jimmy', 'head')
list.insert('xuexue', 'jimmy')
console.log('---------')
list.display()
}{
class Node {
constructor(public element: any = null, public next: Node | null = null) {}
}
class LinkList<T> {
public head = new Node('head')
constructor() {
this.head.next = this.head
}
find(item: T): Node {
let currNode = this.head
while (currNode.next && currNode.next.element !== 'head') {
if (currNode.element === item) {
break
} else {
currNode = currNode.next
}
}
return currNode
}
findPrevious(item: T): Node {
// 查找一个元素的前一个元素
let currNode = this.head
while (currNode.next) {
if (currNode.next.element === item) {
break
} else {
currNode = currNode.next
}
}
return currNode
}
insert(newElement: T, item: T): void {
let node = new Node(newElement)
let currNode = this.find(item)
node.next = currNode.next
currNode.next = node
}
remove(item: T): void {
let prevNode = this.findPrevious(item)
if (prevNode.next) {
prevNode.next = prevNode.next.next
}
}
display(): void {
let currNode = this.head
while (currNode.next) {
console.log(currNode.element)
if (currNode.next && currNode.next.element !== 'head') {
currNode = currNode.next
} else {
break
}
}
}
}
let list = new LinkList<string>()
list.insert('Jimmy', 'head')
list.insert('xuexue', 'jimmy')
console.log('---------')
list.display()
}所以如果是循环链表,我们使用 while 循环遍历链表的时候一定要注意在合适的情况结束循环,否则将是一个死循环。
例题
传说在公元 1 世纪的犹太战争中,犹太历史学家弗拉维奥·约瑟夫斯和他的 40 个同胞被罗马士兵包围。犹太士兵决定宁可自杀也不做俘虏,于是商量出了一个自杀方案。他们围成一个圈,从一个人开始,数到第三个人时将第三个人杀死,然后再数,直到杀光所有人。约瑟夫和另外一个人决定不参加这个疯狂的游戏,他们快速地计算出了两个位置,站在那里得以幸存。写一段程序将 n 个人围成一圈,并且第 m 个人会被杀掉,计算一圈人中哪两个人最后会存活。使用循环链表解决该问题。
解答
我们需要使用循环链表,先初始化一个循环链表,再一次插入 2-39 个元素(头表示的就是第一个),之后再不断的进行删除,判断最后剩下的是哪两个元素。
ts
let list = new LinkList<number>()
list.insert(2, 1)
for (let i = 3; i <= 40; i++) {
list.insert(i, i - 1)
}
const killOne = (list: LinkList<number>) => {
let start = list.head
while (list.length >= 3) {
if (list.head.next?.next) {
let current = start.next?.next as Node
start = current?.next as Node
list.head = start
list.remove(current.element)
}
}
console.log(list.head.element)
console.log(list.head.next.element)
}
killOne(list)let list = new LinkList<number>()
list.insert(2, 1)
for (let i = 3; i <= 40; i++) {
list.insert(i, i - 1)
}
const killOne = (list: LinkList<number>) => {
let start = list.head
while (list.length >= 3) {
if (list.head.next?.next) {
let current = start.next?.next as Node
start = current?.next as Node
list.head = start
list.remove(current.element)
}
}
console.log(list.head.element)
console.log(list.head.next.element)
}
killOne(list)我也不知道我的理解的是否有错,第一个杀的是 3 然后 6 然后 9.....最后剩下的是就是活下来的人。
散列表(hashTable)
散列表对于我来说是一个全新的知识点,其他的数据结构像栈、队列、链表之类的或多或少在大学里都听过,所以再看这块的知识就跟复习一样,而散列表的知识第一次看知识点感觉好新颖,有点像是对象的底层实现。所以为了更好的理解散列表,我们要暂时忘记想象 JS 并没有给我们提供可以存储键值对的 Map 类型对象,而是需要我们自己实现一个可以存储键值对的数据结构!
这里散列表是基于数组来实现的,我理解的它最重要的是用来让我们存储一些键值对(先忽略为什么用数组实现键值对,我刚开始也很疑惑,最重要的是理解这个设计的思想)
实现散列表需要知道的一个名词是 碰撞,理解这个词先要知道散列表到底是做的是啥,咋存储的。
简单的说就是创建一个容量大小预先设定的数组,之后通过一个特殊的算法,将我们要存储的每个 key,都转成一一对应的数值,之后将这个数值作为数组的下标,键值对的值作为这个下标下所存储的值。所以碰撞表示的是:两个不同 key 通过算法处理之后对应的是同一个数字,后面被作为数组的索引存储我们的数组中。
我个人觉得能够手写散列表固然很牛逼很加分,但是了解基础的数据结构算法是更加重要的。
简单实现
ts
{
class HashTable {
/**
* 这里数组使用的是定容数组,而且数组的大小是一个质数
* 因为会需要数组的容量进行处理散列算法,所以 质数 很关键
*/
public table: any[] = new Array(137)
// 简单的散列函数(真实的这个函数肯定是非常复杂的,这里我的意思是大致模拟一下)
private simpHash(data: any): number {
// 霍纳算法
const H = 37
var total = 0
for (var i = 0; i < data.length; ++i) {
total += H * total + data.charCodeAt(i)
}
total = total % this.table.length
if (total < 0) {
total += this.table.length - 1
}
return parseInt(total as unknown as string)
}
// 插入元素
public put(data: any, value: any) {
// 通过这里也可以知道 散列函数是非常重要的,一定要确保的是不发生碰撞
let index = this.simpHash(data)
this.table[index] = value
}
// 显示散列表中的元素
public showDistro() {
for (var i = 0; i < this.table.length; ++i) {
if (this.table[i] != undefined) {
console.log(i + ': ' + this.table[i])
}
}
}
// 获取值
public get(key: any): any {
return this.table[this.simpHash(key)]
}
}
let table1 = new HashTable()
table1.put('Jimmy', 111)
table1.put('xuexue', 222)
table1.put('Jack', 333)
table1.put('Henry', 444)
table1.put(22, 444)
table1.put('22', 'what')
table1.showDistro()
}{
class HashTable {
/**
* 这里数组使用的是定容数组,而且数组的大小是一个质数
* 因为会需要数组的容量进行处理散列算法,所以 质数 很关键
*/
public table: any[] = new Array(137)
// 简单的散列函数(真实的这个函数肯定是非常复杂的,这里我的意思是大致模拟一下)
private simpHash(data: any): number {
// 霍纳算法
const H = 37
var total = 0
for (var i = 0; i < data.length; ++i) {
total += H * total + data.charCodeAt(i)
}
total = total % this.table.length
if (total < 0) {
total += this.table.length - 1
}
return parseInt(total as unknown as string)
}
// 插入元素
public put(data: any, value: any) {
// 通过这里也可以知道 散列函数是非常重要的,一定要确保的是不发生碰撞
let index = this.simpHash(data)
this.table[index] = value
}
// 显示散列表中的元素
public showDistro() {
for (var i = 0; i < this.table.length; ++i) {
if (this.table[i] != undefined) {
console.log(i + ': ' + this.table[i])
}
}
}
// 获取值
public get(key: any): any {
return this.table[this.simpHash(key)]
}
}
let table1 = new HashTable()
table1.put('Jimmy', 111)
table1.put('xuexue', 222)
table1.put('Jack', 333)
table1.put('Henry', 444)
table1.put(22, 444)
table1.put('22', 'what')
table1.showDistro()
}哈希表和红黑树
前面已经知道了哈希表是可以用来实现存储键值对这种数据类型的结构了,但是本质上除了哈希表以外,还有其他的数据结构也可以用来实现键值对的存储,就是 红黑树,这个知识点这本书我看到现在还有没有出现这个数据结构,之所以我会知道这个是因为在和一个算法大厂的同学聊天中得知的,C++这门语言有专门提供两种 Map 类型的键值对,底层分别是使用哈希表和红黑树!
集合(Set)
虽然 JS 在 ES6 版本已经给我们提供了实现集合的构造函数Set,但是这本书是在 ES6 之前就出的了,所以可见集合这个数据类型/结构是非常重要的,所以也就跟着手动实现一个集合吧~
在过于说到 Set 我的第一想法就是数组去重,诚然这是个非常有用的操作,面试也蛮经常会问到的,但是正所谓集合,如数学上的集合,我们经常处理的就是,交集、并集、差集、子集操作。
列表具有以下的 API:
| 属性/方法 | 含义 |
|---|---|
| size(属性) | 集合的元素个数 |
| add(方法) | 添加元素 |
| remove(方法) | 删除元素 |
| union(方法) | 并集操作 |
| intersect(方法) | 交集操作 |
| difference(方法) | 差集操作 |
| subset(方法) | 判断当前的集合是否指定集合的子集 |
| show(方法) | 输出集合成员 |
简单实现
ts
{
class Set {
private dataStore: any[] = []
constructor() {}
get size() {
return 11
}
public add(item: any): boolean {
if (!this.dataStore.includes(item)) {
this.dataStore.push(item)
return true
}
return false
}
public remove(item: any): boolean {
let index = this.dataStore.indexOf(item)
if (index !== -1) {
this.dataStore.splice(index, 1)
return true
}
return false
}
// 并集操作
public union(set: Set) {
let tempSet = new Set()
for (let i = 0; i < this.dataStore.length; i++) {
tempSet.add(this.dataStore[i])
}
for (let j = 0; j < set.size; j++) {
if (!tempSet.contains(set.dataStore[i])) {
tempSet.dataStore.push(set.dataStore[i])
}
}
return tempSet
}
// 交集操作
public intersect(set: Set) {
let tempSet = new Set()
for (let i = 0; i < this.dataStore.length; i++) {
if (set.contains(this.dataStore[i])) {
tempSet.add(this.dataStore[i])
}
}
}
// 差集
public difference(set: Set) {
let tempSet = new Set()
for (let i = 0; i < this.dataStore.length; i++) {
if (!set.contains(this.dataStore[i])) {
tempSet.add(this.dataStore[i])
}
}
}
// 判断当前的集合是否指定集合的子集
public subset(set: Set): boolean {
if (set.size < this.size) {
return false
}
for (const value of this.dataStore) {
if (!set.contains(value)) {
return false
}
}
return true
}
public show() {
this.dataStore.forEach(item => console.log(item))
}
// 工具方法 判断一个元素书否存在于一个集合中
private contains(item: any) {
if (this.dataStore.includes(item)) {
return true
} else {
return false
}
}
}
let set = new Set()
set.add('jimmy')
set.add('xuexue')
console.log(set.remove('jimy'))
console.log(set)
let set2 = new Set()
set2.add('jimmy')
console.log(set2.subset(set))
}{
class Set {
private dataStore: any[] = []
constructor() {}
get size() {
return 11
}
public add(item: any): boolean {
if (!this.dataStore.includes(item)) {
this.dataStore.push(item)
return true
}
return false
}
public remove(item: any): boolean {
let index = this.dataStore.indexOf(item)
if (index !== -1) {
this.dataStore.splice(index, 1)
return true
}
return false
}
// 并集操作
public union(set: Set) {
let tempSet = new Set()
for (let i = 0; i < this.dataStore.length; i++) {
tempSet.add(this.dataStore[i])
}
for (let j = 0; j < set.size; j++) {
if (!tempSet.contains(set.dataStore[i])) {
tempSet.dataStore.push(set.dataStore[i])
}
}
return tempSet
}
// 交集操作
public intersect(set: Set) {
let tempSet = new Set()
for (let i = 0; i < this.dataStore.length; i++) {
if (set.contains(this.dataStore[i])) {
tempSet.add(this.dataStore[i])
}
}
}
// 差集
public difference(set: Set) {
let tempSet = new Set()
for (let i = 0; i < this.dataStore.length; i++) {
if (!set.contains(this.dataStore[i])) {
tempSet.add(this.dataStore[i])
}
}
}
// 判断当前的集合是否指定集合的子集
public subset(set: Set): boolean {
if (set.size < this.size) {
return false
}
for (const value of this.dataStore) {
if (!set.contains(value)) {
return false
}
}
return true
}
public show() {
this.dataStore.forEach(item => console.log(item))
}
// 工具方法 判断一个元素书否存在于一个集合中
private contains(item: any) {
if (this.dataStore.includes(item)) {
return true
} else {
return false
}
}
}
let set = new Set()
set.add('jimmy')
set.add('xuexue')
console.log(set.remove('jimy'))
console.log(set)
let set2 = new Set()
set2.add('jimmy')
console.log(set2.subset(set))
}二叉树
树是计算机科学中经常用到的一种数据结构,二叉树是最为特殊的一种树的结构。是因为在二叉树上进行查找非常快(而在链表上查找则不是这样),为二叉树添加或删除元素也非常快(而对数组执行添加或删除操作则不是这样)。
- 链表查找元素的效率不高(一定要找到一个节点的前驱节点才能获取到当前节点)
- 数组添加和删除元素效率 可能 不高(在数组头部删除和添加元素效率不高)
树的数据结构不仅非常广泛的运用于计算机世界中,生活中也是普遍使用到,如公司的组织架构:
二叉树是一种特殊的树,它的子节点个数不超过两个。二叉树具有一些特殊的计算性质,使得在它们之上的一些操作异常高效。
二叉搜索树(BST)
BST:Binary Sort Tree
二叉查找树是一种特殊的二叉树,相对较小的值保存在左节点中,较大的值保存在右节点中。其的定义:
- 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
- 左、右子树也分别为二叉排序树;
列表具有以下的 API:
| 属性/方法 | 含义 |
|---|---|
| root(属性) | 树的根节点 |
| insert(方法) | 添加元素 |
| remove(方法) | 删除元素 |
| find(方法) | 查找元素 |
| getMin(方法) | 获取最小的值 |
| getMax(方法) | 获取最大值 |
| preOrder(方法) | 先序遍历 |
| inOrder(方法) | 中序遍历 |
| postOrder(方法) | 后序遍历 |
正常的二叉树是获取数中的最大值和最小值是相对比较费时间的,但是由于二叉搜索树的特性,我们获取最大值和最小值就非常的快速:
- 最小值往左下角查找
- 最大值往右下角查找
其次二叉树需要掌握的是 先序遍历、中序遍历、后序遍历,正常的方式是通过递归的方式可以实现,当然也可以使用while(true)这种循环的方式实现!
二叉搜索树比较特殊,插入元素的时候也需要满足搜索树的条件,小值放左边,大值放右边
二叉搜索数删除在删除的时候也需要做特别的处理!!!
- 如果待删除节点是叶子节点(没有子节点的节点),那么只需要将从父节点指向它的链接 指向 null。
- 如果待删除节点只包含一个子节点,那么原本指向它的节点久得做些调整,使其指向它的 子节点。
- 如果待删除节点包含两个子节点,正确的做法有两种:要么查找待删除节点左子树 上的最大值,要么查找其右子树上的最小值。(下面的代码实现使用的是第二种)
Node
ts
class Node {
constructor(
public data: number | null = null,
public Left: Node | null = null,
public right: Node | null = null
) {}
public show(): number | null {
return this.data
}
}class Node {
constructor(
public data: number | null = null,
public Left: Node | null = null,
public right: Node | null = null
) {}
public show(): number | null {
return this.data
}
}BST
ts
class BST {
constructor(public root: Node | null = null) {}
public insert(data: number) {
let node = new Node(data, null, null)
// 如果根为空 直接插入
if (this.root === null) {
this.root = node
return
}
// 根据二叉搜索树规则插入
let current = this.root
let parent
while (true) {
parent = current
if (parent.data && data < parent.data) {
current = current.Left as Node
if (!current) {
parent.Left = node
break
}
} else {
current = current.right as Node
if (!current) {
parent.right = node
break
}
}
}
}
// 先序遍历
public preOrder(root: Node) {
if (root) {
console.log(root.data)
this.preOrder(root.Left as Node)
this.preOrder(root.right as Node)
}
}
// 中序遍历
public inOrder(root: Node) {
if (root) {
this.inOrder(root.Left as Node)
console.log(root.data)
this.inOrder(root.right as Node)
}
}
// 后续遍历
public postOrder(root: Node) {
if (root) {
this.postOrder(root.Left as Node)
this.postOrder(root.right as Node)
console.log(root.data)
}
}
// 获取最小值
public getMin(): number {
let current = this.root
while (current && current.Left) {
current = current.Left
}
return (current && current.data) as number
}
// 获取最大值
public getMax(): number {
let current = this.root
while (current && current.right) {
current = current.right
}
return (current && current.data) as number
}
// 查找节点
public find(data: number): Node | null {
let current = this.root
while (current) {
if (current && current.data === data) {
return current
} else if (current && (current.data as number) < data) {
current = current.right
} else if (current && (current.data as number) > data) {
current = current.Left
}
}
return null
}
// 删除节点
public remove(data: number) {
this.root = this.removeNode(this.root as Node, data)
}
private removeNode(node: Node, data: number): Node | null {
if (!node) {
return null
}
if (data === node.data) {
// 叶子节点
if (!node.Left && !node.right) {
return null
}
// 没有左节点
if (!node.Left) {
return node.right
}
// 没有右节点
if (!node.right) {
return node.Left
}
// 有两个子节点的节点
let tempNode = this.getMinNode(node.right)
node.data = tempNode.data
node.right = this.removeNode(node.right, tempNode.data as number)
return node
} else if (data < (node.data as number)) {
node.Left = this.removeNode(node.Left as Node, data)
return node
} else {
node.right = this.removeNode(node.right as Node, data)
return node
}
}
private getMinNode(node: Node): Node {
let current = node
while (current && current.Left) {
current = current.Left
}
return current
}
}
let nums = new BST()
// nums.root
nums.insert(23)
nums.insert(45)
nums.insert(16)
nums.insert(37)
nums.insert(3)
nums.insert(99)
nums.insert(22)
// nums.inOrder(nums.root as Node)
nums.preOrder(nums.root as Node)
// nums.postOrder(nums.root as Node)
console.log('min', nums.getMin())
console.log('max', nums.getMax())
console.log('find', nums.find(7))
nums.remove(23)
// nums.preOrder(nums.root as Node)
// nums.inOrder(nums.root as Node)class BST {
constructor(public root: Node | null = null) {}
public insert(data: number) {
let node = new Node(data, null, null)
// 如果根为空 直接插入
if (this.root === null) {
this.root = node
return
}
// 根据二叉搜索树规则插入
let current = this.root
let parent
while (true) {
parent = current
if (parent.data && data < parent.data) {
current = current.Left as Node
if (!current) {
parent.Left = node
break
}
} else {
current = current.right as Node
if (!current) {
parent.right = node
break
}
}
}
}
// 先序遍历
public preOrder(root: Node) {
if (root) {
console.log(root.data)
this.preOrder(root.Left as Node)
this.preOrder(root.right as Node)
}
}
// 中序遍历
public inOrder(root: Node) {
if (root) {
this.inOrder(root.Left as Node)
console.log(root.data)
this.inOrder(root.right as Node)
}
}
// 后续遍历
public postOrder(root: Node) {
if (root) {
this.postOrder(root.Left as Node)
this.postOrder(root.right as Node)
console.log(root.data)
}
}
// 获取最小值
public getMin(): number {
let current = this.root
while (current && current.Left) {
current = current.Left
}
return (current && current.data) as number
}
// 获取最大值
public getMax(): number {
let current = this.root
while (current && current.right) {
current = current.right
}
return (current && current.data) as number
}
// 查找节点
public find(data: number): Node | null {
let current = this.root
while (current) {
if (current && current.data === data) {
return current
} else if (current && (current.data as number) < data) {
current = current.right
} else if (current && (current.data as number) > data) {
current = current.Left
}
}
return null
}
// 删除节点
public remove(data: number) {
this.root = this.removeNode(this.root as Node, data)
}
private removeNode(node: Node, data: number): Node | null {
if (!node) {
return null
}
if (data === node.data) {
// 叶子节点
if (!node.Left && !node.right) {
return null
}
// 没有左节点
if (!node.Left) {
return node.right
}
// 没有右节点
if (!node.right) {
return node.Left
}
// 有两个子节点的节点
let tempNode = this.getMinNode(node.right)
node.data = tempNode.data
node.right = this.removeNode(node.right, tempNode.data as number)
return node
} else if (data < (node.data as number)) {
node.Left = this.removeNode(node.Left as Node, data)
return node
} else {
node.right = this.removeNode(node.right as Node, data)
return node
}
}
private getMinNode(node: Node): Node {
let current = node
while (current && current.Left) {
current = current.Left
}
return current
}
}
let nums = new BST()
// nums.root
nums.insert(23)
nums.insert(45)
nums.insert(16)
nums.insert(37)
nums.insert(3)
nums.insert(99)
nums.insert(22)
// nums.inOrder(nums.root as Node)
nums.preOrder(nums.root as Node)
// nums.postOrder(nums.root as Node)
console.log('min', nums.getMin())
console.log('max', nums.getMax())
console.log('find', nums.find(7))
nums.remove(23)
// nums.preOrder(nums.root as Node)
// nums.inOrder(nums.root as Node)图(graph)
图对我来说也是一个全新的数据结构,以前从未接触过图,现实中图的例子也有蛮多,铁路图、交通干线图这都是图的结构,在计算机世界中经过了解发现前端日常使用的最多的一个工具之一“webpack,在打包构建的时候其实也是有使用到图的数据结构的,各个文件之间的依赖关系就是一个图的数据结构。
图最重要的元素:定点、边
根据图是否有方向可以分为:有向图、无方向图
根据图的边是否带值(权重)可分为:带权图、不带权图
表示图的方式:邻接表(邻接表数组)
- 邻接表(邻接表数组)
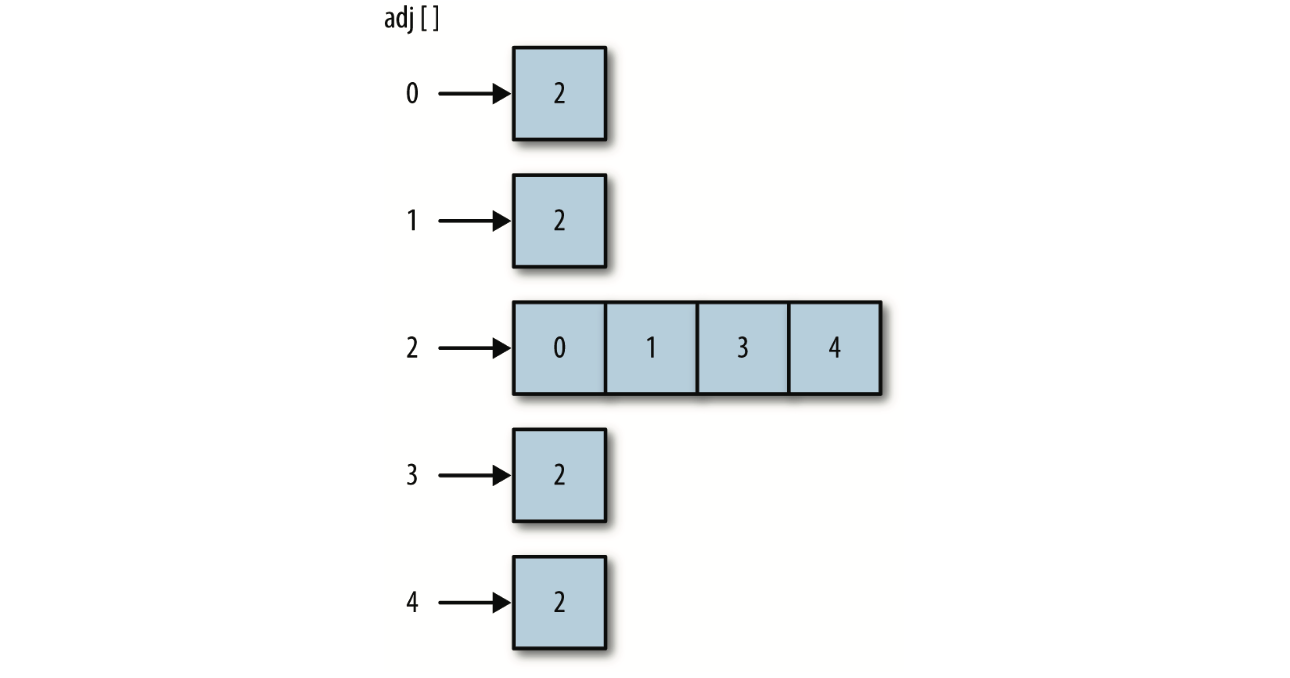
关于图的两种算法:深度优先搜索(dfs)、广度优先搜索(bfs)
深度优先搜素
深度优先搜索算法比较简单:访问一个没有访问过的顶点,将它标记为已访问,再递归地去访问在初始顶点的邻接表中其他没有访问过的顶点。
ts
class Graph {
edges = 0 // 边
adj: (string | number)[][] = []
constructor(public vertices = 0) {
for (let i = 0; i < this.vertices; i++) {
this.adj[i] = []
this.adj[i].push('') // 自己不可能和自己相连
}
}
addEdge(v: number, w: number) {
this.adj[v].push(w)
this.adj[w].push(v)
this.edges++
}
showGraph() {
for (let i = 0; i < this.vertices; i++) {
console.log(i + '->')
for (let j = 0; j < this.vertices; j++) {
if (this.adj[j][j] !== undefined) {
console.log(this.adj[i][j])
}
}
console.log('--------')
}
}
}
let g = new Graph(5)
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 3)
g.addEdge(2, 4)
g.showGraph()class Graph {
edges = 0 // 边
adj: (string | number)[][] = []
constructor(public vertices = 0) {
for (let i = 0; i < this.vertices; i++) {
this.adj[i] = []
this.adj[i].push('') // 自己不可能和自己相连
}
}
addEdge(v: number, w: number) {
this.adj[v].push(w)
this.adj[w].push(v)
this.edges++
}
showGraph() {
for (let i = 0; i < this.vertices; i++) {
console.log(i + '->')
for (let j = 0; j < this.vertices; j++) {
if (this.adj[j][j] !== undefined) {
console.log(this.adj[i][j])
}
}
console.log('--------')
}
}
}
let g = new Graph(5)
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 3)
g.addEdge(2, 4)
g.showGraph()动态规划
很多时候我们会使用递归去解决问题,比如计算斐波那契数列,大多数时候我们第一想法都是使用递归,但是递归的效率其实是不高的,甚至可以说是效率比较低下,现在我知道了,许多使用递归去解决的问题没大部分都可以重写为使用动态规划进行解题!
为什么我们钟爱递归
还是那个斐波那契数列的例子,我们如果使用递归去实现,代码大致是如下:
js
function recurFib(n){
if(n < 2){
return n
}else{
return recurFib(n-1) + recurFib(n-2)
}
}function recurFib(n){
if(n < 2){
return n
}else{
return recurFib(n-1) + recurFib(n-2)
}
}代码的逻辑结构非常的清晰!这就是递归的优势,看代码就特别好理解,但是实际上递归的效率不高,看下它执行的图就知道了:
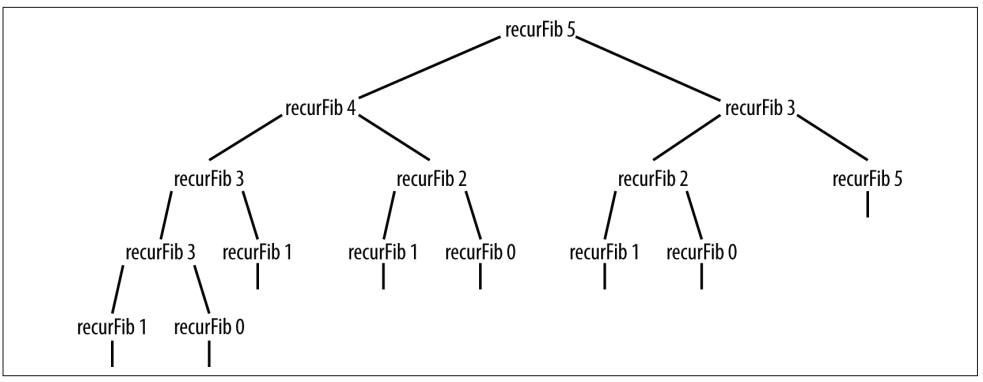
又比较多无用的计算,而且递归每次执行都会在进程栈中插入一个函数,如果我们没写好就很容易出现死循环!
动态规划巧解
这一词我的理解是,我们可以自己预知程序后面的走向结果,所以我们不需要去计算过程,只需要把每一步的结果都大致的计算出来。
还是拿斐波那契数列来举例子:
第一项:0
第二项:1
第三项:1
第四项:2
第五项:3
......
就是数组:[0,1,1,2,3]
所以我们如果要知道第n项,就只要知道n-1项和n-2项就可以了,所以我们可以从头到尾把值写出来
js
function dyFib(n){
const arr = []
// 先初始化数组
for(let i = 0;i < n;i++){
arr[i] = 0
}
if(n === 1||n===2){
return 1
}else{
// 给数组的每一项都赋值
arr[1] = 1
arr[2] = 1
for(let i = 3;i<n;i++){
arr[i] = arr[i-1]+arr[i-2]
}
// 取出数组的最后一项
return arr[n-1]
}
}function dyFib(n){
const arr = []
// 先初始化数组
for(let i = 0;i < n;i++){
arr[i] = 0
}
if(n === 1||n===2){
return 1
}else{
// 给数组的每一项都赋值
arr[1] = 1
arr[2] = 1
for(let i = 3;i<n;i++){
arr[i] = arr[i-1]+arr[i-2]
}
// 取出数组的最后一项
return arr[n-1]
}
}以上代码可以看出来,至始至终我们都在做赋值操作,数组的赋值操作时极快的,所以它的效率自然时非常的给力,尤其时在当n 越大时,优化效果越加明显!
总结
递归和动态规划他们的本质区别大致如下(我的理解):
递归和动态规划时孪生兄弟,能用递归的地方一般也都可以使用动态规划!
递归像是从后往前计算
动态规划像是递归逆运算,效率更高
递归会有比较多的无效计算,这是其效率不高的主要原因
理解到这就差不多了,重要的是今后在遇到递归的场景时,可以试着看看能不能用动态规划解题,不要一股脑i子图方便就去用递归解题了!
 前端加油站🧠
前端加油站🧠