前端加油站🧠

Appearance

下一个排列 ​

考点

难度：中级

思想：排序、循环

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=465391686&bvid=BV1pL411V7me&cid=476632469&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=465391686&bvid=BV1pL411V7me&cid=476632469&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

实现获取 下一个排列 的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列（即，组合出下一个更大的整数）。

如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

必须 原地 修改，只允许使用额外常数空间。

示例 1：

输入：nums = [1,2,3] 输出：[1,3,2] 示例 2：

输入：nums = [3,2,1] 输出：[1,2,3] 示例 3：

输入：nums = [1,1,5] 输出：[1,5,1] 示例 4：

输入：nums = [1] 输出：[1]。

解题思路 ​

首先这题有给我们一些重要的限制

  • 数组只能 原地修改
    • 排序
    • 两两交换
  • 只允许额外的 常数空间

解题原型：

image-20220103133005660

总结步骤有以下几步：

  • 从后往前遍历数组，当前遍历的这个值比前一个值（i - 1）大的情况
  • 如果找到了停止遍历，将这个值及其以后的值进行 升序 排序
  • 在 升序 的这个数组中再遍历，找到一个比 索引为(i-1)值大的数，将这两个数进行两两交换。

细节：

  • 有关数组的操作全部都要在原数组中操作，不能生成额外的数组
  • 需要写一些简单的排序算法

其他

文档资料请到：http://www.jimmyxuexue.top:999/

源码请到公众号：Jimmy 前端 中获取

image-20220101163759472

两两交换链表中的节点 ​

考点

难度：中级

思想：链表

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=935351395&bvid=BV18T4y127j1&cid=474874163&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=935351395&bvid=BV18T4y127j1&cid=474874163&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

题目 ​

:::

输入：head = [1,2,3,4] 输出：[2,1,4,3] 示例 2：

输入：head = [] 输出：[] 示例 3：

输入：head = [1] 输出：[1]

解题思路 ​

如果是数组？是不是就很简单了？ ​

[1,2,3,4] = > [2,1,4,3]

思路：

  • 每两个两个进行一次交换

    • index%2 === 0 为一对交换元素中的第一个

    • index%2 !==0 为一堆交换元素中的第二个

    • 两两交换的基本代码（需要引入一个 temp 临时变量）

      js
      let a = 1,
	b = 2
let temp = a
a = b
b = a
      let a = 1,
	b = 2
let temp = a
a = b
b = a

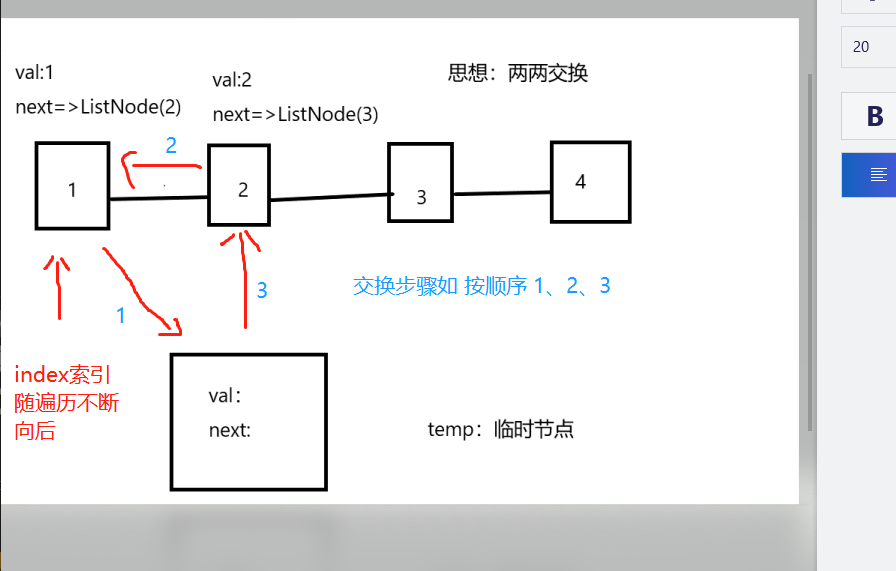
链表也是一样，只是链表的数据结构有所不同 ​

链表每个节点存储的是一个对象，分别存储着 val 值和 next 索引，next 指向的就是下一个节点

思路和数组一样，遍历链表，每两个链表作为一对交换的点，再进行亮亮交换

image-20220101163517745

具体代码

js
/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var swapPairs = function (head) {
	let demo = head
	let index = 0
	let temp = new ListNode(null)
	while (demo) {
		if (index % 2 === 0) {
			temp.val = demo.val
			if (demo.next) {
				demo.val = demo.next.val
			}
		} else {
			demo.val = temp.val
		}
		index++
		demo = demo.next
	}
	return head
}
/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var swapPairs = function (head) {
	let demo = head
	let index = 0
	let temp = new ListNode(null)
	while (demo) {
		if (index % 2 === 0) {
			temp.val = demo.val
			if (demo.next) {
				demo.val = demo.next.val
			}
		} else {
			demo.val = temp.val
		}
		index++
		demo = demo.next
	}
	return head
}

总结 ​

使用数组的解决思路放到链表上即可，只是因为数据结构不同，代码略有不同，但是思想是一样的。

两数相除 ​

考点

难度：中级

思想：递归、循环

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=765364749&bvid=BV1Zr4y1m74w&cid=475644754&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=765364749&bvid=BV1Zr4y1m74w&cid=475644754&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

给定两个整数，被除数 dividend 和除数 divisor。将两数相除，要求不使用乘法、除法和 mod 运算符。

返回被除数 dividend 除以除数 divisor 得到的商。

整数除法的结果应当截去（truncate）其小数部分，例如：truncate(8.345) = 8 以及 truncate(-2.7335) = -2

示例 1:

输入: dividend = 10, divisor = 3 输出: 3 解释: 10/3 = truncate(3.33333..) = truncate(3) = 3 示例 2:

输入: dividend = 7, divisor = -3 输出: -2 解释: 7/-3 = truncate(-2.33333..) = -2

解题思路 ​

首先声明我的这个解题肯定不是最优解！这题比较难只能是先写出来打个标记日后再回来以更优的方式重做。

我的思路就是正常的数学思路解题，使用循环或者递归进行解题。

我们需要注意性能问题以及考虑的点：

  • 当被除数为 0 时，直接 0
  • 因为被除数和除数可能为负数，所以需要考虑 - - 负负得正，负正得负，正正得正
  • 获取负数的个数
  • 利用循环/递归的方式进行累加/累乘进行解题

搜索旋转排序数组 ​

考点

难度：中级

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=850413721&bvid=BV1aL4y1t75Q&cid=477449479&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=850413721&bvid=BV1aL4y1t75Q&cid=477449479&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0 输出：4 示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3 输出：-1 示例 3：

输入：nums = [1], target = 0 输出：-1

解题思路 ​

因为整个数组最对会被分成两个相对升序的数组

因为数组是升序的，所以我们在查找值时其实是有方法，在满足条件情况下就不用继续遍历了，所以总体上就是我们要规避掉不需要的操作

解题原型：

  • 场景 1：小 => 大 => 小

    image-20220104192304623

  • 场景 2：大 => 小

    image-20220104191403019

  • 场景 3

    直接找到 target 指数输出即可

总结步骤有以下几步：

我们需要比对 目标值 和 遍历中的每个值的大小情况

  • 当相等时，直接输出这个索引

  • 当大小情况出现：小=>大=>小 的情况 不需要遍历 直接返回-1

  • 当大小情况出现：大=>小 的情况 不需要遍历 直接返回-1

细节：

  • 需要定义额外的变量来确定是先小后大，还是先大后小

其他

文档资料请到：http://www.jimmyxuexue.top:999/

源码请到公众号：Jimmy 前端 中获取

有效的数独 ​

考点

难度：中级

思想：遍历、数据处理

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=423008586&bvid=BV1r3411e7Fx&cid=480740745&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=423008586&bvid=BV1r3411e7Fx&cid=480740745&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

注意：

一个有效的数独（部分已被填充）不一定是可解的。 只需要根据以上规则，验证已经填入的数字是否有效即可。 空白格用 '.' 表示。

js
示例 1：

输入：board =
[
   ["5","3",".",".","7",".",".",".","."]
  ,["6",".",".","1","9","5",".",".","."]
  ,[".","9","8",".",".",".",".","6","."]
  ,["8",".",".",".","6",".",".",".","3"]
  ,["4",".",".","8",".","3",".",".","1"]
  ,["7",".",".",".","2",".",".",".","6"]
  ,[".","6",".",".",".",".","2","8","."]
  ,[".",".",".","4","1","9",".",".","5"]
  ,[".",".",".",".","8",".",".","7","9"]
]
输出：true
示例 2：

输入：board =
[
   ["8","3",".",".","7",".",".",".","."]
  ,["6",".",".","1","9","5",".",".","."]
  ,[".","9","8",".",".",".",".","6","."]
  ,["8",".",".",".","6",".",".",".","3"]
  ,["4",".",".","8",".","3",".",".","1"]
  ,["7",".",".",".","2",".",".",".","6"]
  ,[".","6",".",".",".",".","2","8","."]
  ,[".",".",".","4","1","9",".",".","5"]
  ,[".",".",".",".","8",".",".","7","9"]
]
输出：false
示例 1：

输入：board =
[
   ["5","3",".",".","7",".",".",".","."]
  ,["6",".",".","1","9","5",".",".","."]
  ,[".","9","8",".",".",".",".","6","."]
  ,["8",".",".",".","6",".",".",".","3"]
  ,["4",".",".","8",".","3",".",".","1"]
  ,["7",".",".",".","2",".",".",".","6"]
  ,[".","6",".",".",".",".","2","8","."]
  ,[".",".",".","4","1","9",".",".","5"]
  ,[".",".",".",".","8",".",".","7","9"]
]
输出：true
示例 2：

输入：board =
[
   ["8","3",".",".","7",".",".",".","."]
  ,["6",".",".","1","9","5",".",".","."]
  ,[".","9","8",".",".",".",".","6","."]
  ,["8",".",".",".","6",".",".",".","3"]
  ,["4",".",".","8",".","3",".",".","1"]
  ,["7",".",".",".","2",".",".",".","6"]
  ,[".","6",".",".",".",".","2","8","."]
  ,[".",".",".","4","1","9",".",".","5"]
  ,[".",".",".",".","8",".",".","7","9"]
]
输出：false

解释：除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例 1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

解题思路 ​

这种题目应该是有巧解的方法的，我试着根据思路进行解题，最终发现算法的内存消耗和时间都蛮不错的，所以也记录一下解题思路。

image-20220109161407447

根据数独的游戏规则，我们需要判断：

  • 数字 1-9 在每一行只能出现一次。
  • 数字 1-9 在每一列只能出现一次。
  • 每个九宫格内数字 1-9 只能出现一次

行和列都相对好做，只需遍历二位数组时稍加判断即可，相对复杂一点的是如何处理 9 宫格的数字，在这题中，我们需要借助坐标来进行判断，将每个点拆解为如下的坐标：

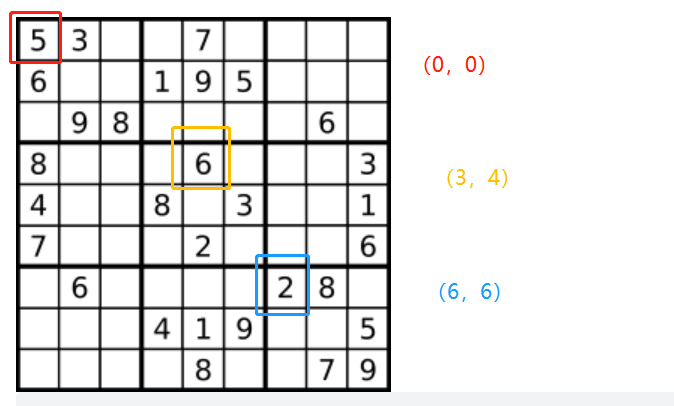
image-20220109162713756

然后做以下几件事：

  • 处理之前先初始化好一个二维数组 [[], [], [], [], [], [], [], [], []],存放每个格子的元素

  • 然后将 行和列分别除 3 之后 根据行和列的值进行判断应该插入到具体的哪个数组中 根据 行*3+列 这个公式

    如：（5，5）这个点 计算之后 行=1 列=1 根据公式 行\*3+列 = 4 所以应该放入数组的下标 4 的位置（从 0 开始的）

  • 做到这一步就可以解题啦~

源代码 ​

js
/**
 * @param {character[][]} board
 * @return {boolean}
 */
var isValidSudoku = function (board) {
	let rowGap = []
	let colGap = []
	let boxGap = [[], [], [], [], [], [], [], [], []]
	for (let i = 0; i < board.length; i++) {
		// 处理列
		colGap = []
		for (let l = 0; l < board.length; l++) {
			if (board[l][i] !== '.') {
				if (colGap.includes(board[l][i])) {
					return false
				} else {
					colGap.push(board[l][i])
				}
			}
		}

		for (let j = 0; j < board[i].length; j++) {
			// 处理格子
			let m = parseInt(i / 3),
				n = parseInt(j / 3)
			if (board[i][j] !== '.') {
				if (boxGap[m * 3 + n].includes(board[i][j])) {
					return false
				} else {
					boxGap[m * 3 + n].push(board[i][j])
				}
			}
			// 处理行
			if (j === 0) {
				rowGap = []
			}
			if (j <= board[i].length - 1) {
				if (board[i][j] !== '.') {
					if (rowGap.includes(board[i][j])) {
						return false
					} else {
						rowGap.push(board[i][j])
					}
				}
			}
		}
	}
	return true
}
/**
 * @param {character[][]} board
 * @return {boolean}
 */
var isValidSudoku = function (board) {
	let rowGap = []
	let colGap = []
	let boxGap = [[], [], [], [], [], [], [], [], []]
	for (let i = 0; i < board.length; i++) {
		// 处理列
		colGap = []
		for (let l = 0; l < board.length; l++) {
			if (board[l][i] !== '.') {
				if (colGap.includes(board[l][i])) {
					return false
				} else {
					colGap.push(board[l][i])
				}
			}
		}

		for (let j = 0; j < board[i].length; j++) {
			// 处理格子
			let m = parseInt(i / 3),
				n = parseInt(j / 3)
			if (board[i][j] !== '.') {
				if (boxGap[m * 3 + n].includes(board[i][j])) {
					return false
				} else {
					boxGap[m * 3 + n].push(board[i][j])
				}
			}
			// 处理行
			if (j === 0) {
				rowGap = []
			}
			if (j <= board[i].length - 1) {
				if (board[i][j] !== '.') {
					if (rowGap.includes(board[i][j])) {
						return false
					} else {
						rowGap.push(board[i][j])
					}
				}
			}
		}
	}
	return true
}

括号生成 ​

考点

难度：中级

思想：递归、回溯

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=680331744&bvid=BV1cS4y1T7mX&cid=473737161&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=680331744&bvid=BV1cS4y1T7mX&cid=473737161&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

示例 1：

输入：n = 3

输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

输入：n = 1 输出：["()"]

递归思想：让函数帮我们做一些特别复杂的计算，我们只告诉递归算法在什么时候应该递归，在什么时候应该停止递归

什么时候应该递归？ ​

  • 左括号的数量小于数字 n = 3 时，可以递归

    当左括号的数量少于 n 时，说明可以继续的递归添加左括号或者右括号

  • 右括号数量小于左括号数量时，可以递归

    右括号的数量小于左括号的时候，可以在这个基础上进行添加右括号，至左右括号数量相等

什么时候应该停止递归？ ​

  • 左括号的数量+右括号的数量 === N*2 就应该退出递归

完整代码 ​

js
/**
 * @param {number} n
 * @return {string[]}
 */
var generateParenthesis = function (n) {
	let arr = [] // 存放结果数组
	diff(0, 0, n, '')
	/**
	 * @param {number} left
	 * @param {number} right
	 * @param {number} n
	 * @param {string} str
	 */
	function diff(left, right, n, str) {
		// 什么时候应该退出呢？
		// 左括号的数量+右括号的数量 === N*2 就应该退出递归
		if (left + right === n * 2) {
			arr.push(str)
			return
		}

		// 什么时候应该递归？
		// 左括号的数量小于数字 n = 3 时，可以递归
		if (left < n) {
			//  n == 3 (( =》 (((
			diff(left + 1, right, n, str + '(')
		}

		// 右括号数量小于左括号数量时，可以递归
		if (right < left) {
			//  (() =》 (()) (())( => (())()
			diff(left, right + 1, n, str + ')')
		}
	}
}

generateParenthesis(3) // ["((()))","(()())","(())()","()(())","()()()"]
/**
 * @param {number} n
 * @return {string[]}
 */
var generateParenthesis = function (n) {
	let arr = [] // 存放结果数组
	diff(0, 0, n, '')
	/**
	 * @param {number} left
	 * @param {number} right
	 * @param {number} n
	 * @param {string} str
	 */
	function diff(left, right, n, str) {
		// 什么时候应该退出呢？
		// 左括号的数量+右括号的数量 === N*2 就应该退出递归
		if (left + right === n * 2) {
			arr.push(str)
			return
		}

		// 什么时候应该递归？
		// 左括号的数量小于数字 n = 3 时，可以递归
		if (left < n) {
			//  n == 3 (( =》 (((
			diff(left + 1, right, n, str + '(')
		}

		// 右括号数量小于左括号数量时，可以递归
		if (right < left) {
			//  (() =》 (()) (())( => (())()
			diff(left, right + 1, n, str + ')')
		}
	}
}

generateParenthesis(3) // ["((()))","(()())","(())()","()(())","()()()"]

组合总和 ​

考点

难度：中级

思想：回溯

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=678071060&bvid=BV1Bm4y1D7jJ&cid=482357628&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=678071060&bvid=BV1Bm4y1D7jJ&cid=482357628&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

给你一个 无重复元素 的整数数组  candidates 和一个目标整数  target ，找出  candidates  中可以使数字和为目标数  target 的 所有不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为  target 的不同组合数少于 150 个。

示例  1：

输入：candidates = [2,3,6,7], target = 7 输出：[[2,2,3],[7]] 解释： 2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。 7 也是一个候选， 7 = 7 。 仅有这两种组合。 示例  2：

输入: candidates = [2,3,5], target = 8 输出: [[2,2,2,2],[2,3,3],[3,5]] 示例 3：

输入: candidates = [2], target = 1 输出: [] 示例 4：

输入: candidates = [1], target = 1 输出: [[1]] 示例 5：

输入: candidates = [1], target = 2 输出: [[1,1]]

解题思路 ​

这个也是回溯的基本题，回溯的题目都是基本递归的一个套路，需要记住回溯问题的套路 ， 不断递归，到符合条件的适合退出，且记住在递归的过程中会去掉不符合条件的情况。也就是 “回溯会减支” 这个过程。

本题逻辑，目标值是 target 我们应该是 target 不断的减去数组的每一项， 直到 target 这个值为 0 的情况 则代表的是已经结束的情况 减去每个值时 剩余的值就变成新的 target 当用剩余值再继续执行和剩余数组每个值进行相加，并将减去的值存放进入临时数组

  • 一旦 target 等于 0 时， 说明符合情况 将这个数组存入到这个结果中
  • 一旦 target<要相加的项时 说明不符合继续回溯的情况了，进行 “减支”

原型图

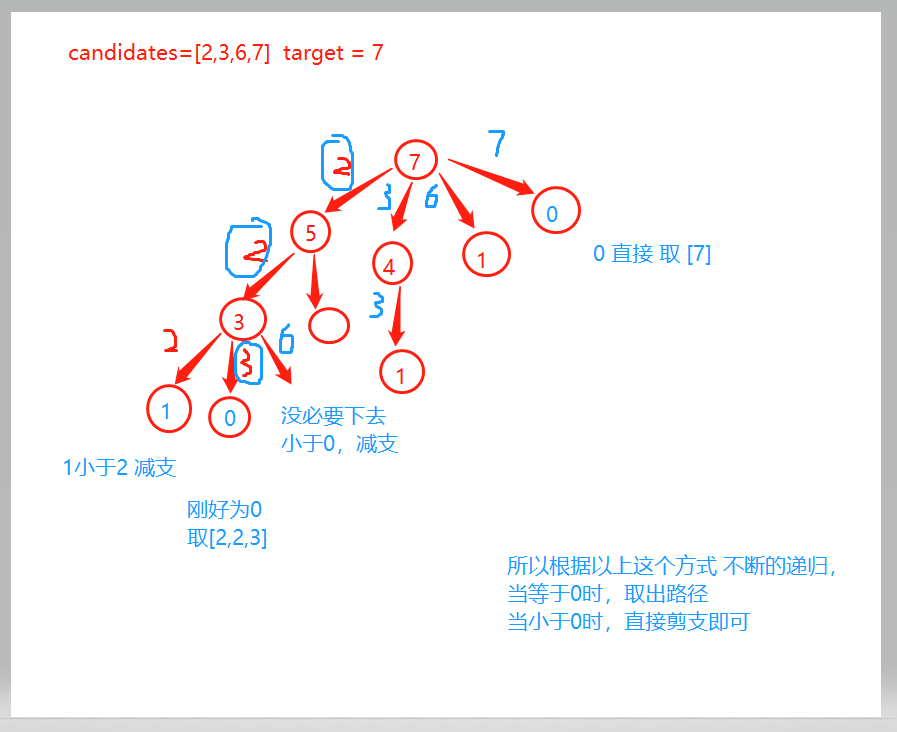
回溯剪支过程

源代码 ​

js
/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum = function (candidates, target) {
	let res = []
	let temp = []
	candidates.sort((a, b) => a - b)
	handleBack(candidates, 0, target)
	function handleBack(arr, start, target) {
		if (target === 0) {
			res.push([...temp])
			return
		}
		for (let i = start; i < arr.length; i++) {
			if (arr[i] > target) break
			temp.push(arr[i]) // 添加一个值 分别将每个值都相加 放入递归函数中执行
			handleBack(arr, i, target - arr[i]) // 将添加一个值的情况进入回溯递归
			temp.pop() // 再去掉这个值 因为这个数组 后面还要加入其他的值  这个非常的关键！！！
		}
	}
	return res
}
/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum = function (candidates, target) {
	let res = []
	let temp = []
	candidates.sort((a, b) => a - b)
	handleBack(candidates, 0, target)
	function handleBack(arr, start, target) {
		if (target === 0) {
			res.push([...temp])
			return
		}
		for (let i = start; i < arr.length; i++) {
			if (arr[i] > target) break
			temp.push(arr[i]) // 添加一个值 分别将每个值都相加 放入递归函数中执行
			handleBack(arr, i, target - arr[i]) // 将添加一个值的情况进入回溯递归
			temp.pop() // 再去掉这个值 因为这个数组 后面还要加入其他的值  这个非常的关键！！！
		}
	}
	return res
}

组合总和 Ⅱ ​

考点

难度：中级

思想：回溯

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=678073980&bvid=BV1zm4y1D7k8&cid=482993426&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=678073980&bvid=BV1zm4y1D7k8&cid=482993426&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

给你一个由候选元素组成的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个元素在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8, 输出: [ [1,1,6], [1,2,5], [1,7], [2,6] ] 示例 2:

输入: candidates = [2,5,2,1,2], target = 5, 输出: [ [1,2,2], [5] ]

解题思路 ​

这题和第 39 题是一样的，都是可以通过回溯的形式进行解题，不断的递归 这题和上一题相比，多的条件是

  • 每个值不能出现重复使用的情况
  • 数组的元素会出现重复

本题逻辑，目标值是 target 我们应该是 target 不断的减去数组的每一项， 直到 target 这个值为 0 的情况 则代表的是已经结束的情况 减去每个值时 剩余的值就变成新的 target 当用剩余值再继续执行和剩余数组每个值进行相加，并将减去的值存放进入临时数组

  • 当前要减的值和前一个值相同的时候，就不需要继续做的直接下一个（这个是因为相同的值重复了）
  • 一旦 target 等于 0 时， 说明符合情况 将这个数组存入到这个结果中
  • 一旦 target<要相加的项时 说明不符合继续回溯的情况了，进行 “减支”

原型图

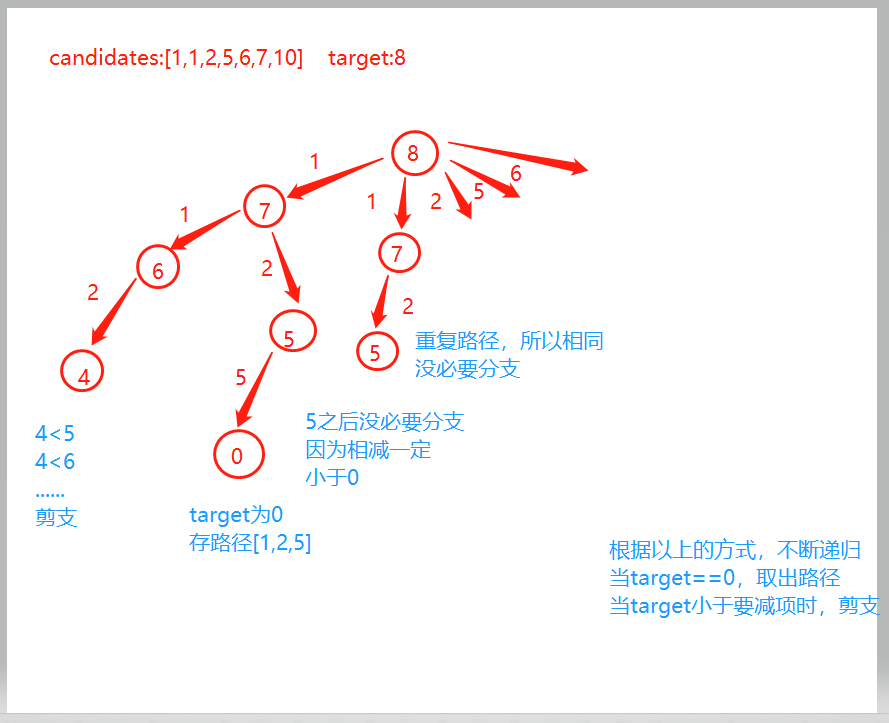
回溯剪支过程

原型图

效果

最终效果

源代码 ​

js
/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum = function (candidates, target) {
	let res = []
	let temp = []
	candidates.sort((a, b) => a - b)
	handleBack(candidates, 0, target)
	function handleBack(arr, start, target) {
		if (target === 0) {
			res.push([...temp])
			return
		}
		for (let i = start; i < arr.length; i++) {
			if (arr[i] > target) break
			if (i > start && arr[i] === arr[i - 1]) {
				// 当前要减的值和上一个值相同时，不需要处理
				continue
			} else {
				temp.push(arr[i])
				handleBack(arr, i + 1, target - arr[i])
				temp.pop()
			}
		}
	}
	return res
}
/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum = function (candidates, target) {
	let res = []
	let temp = []
	candidates.sort((a, b) => a - b)
	handleBack(candidates, 0, target)
	function handleBack(arr, start, target) {
		if (target === 0) {
			res.push([...temp])
			return
		}
		for (let i = start; i < arr.length; i++) {
			if (arr[i] > target) break
			if (i > start && arr[i] === arr[i - 1]) {
				// 当前要减的值和上一个值相同时，不需要处理
				continue
			} else {
				temp.push(arr[i])
				handleBack(arr, i + 1, target - arr[i])
				temp.pop()
			}
		}
	}
	return res
}

全排列 ​

考点

难度：中级

思想：回溯

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=765947112&bvid=BV1Br4y1e7fV&cid=493288637&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=765947112&bvid=BV1Br4y1e7fV&cid=493288637&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3] 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 示例 2：

输入：nums = [0,1] 输出：[[0,1],[1,0]] 示例 3：

输入：nums = [1] 输出：[[1]]

解题思路 ​

本题是一个全排列题目，这题其实和匹配括号是有点像的，可以使用回溯的方式来进行解决！

  • 创建两个数组 一个空数组 一个存放 nums
  • 每次递归都往第一个数组中存放一个 nums 中的一个值 nums 就减去一个值 之后再次进入递归
  • 递归不断执行上面那个过程的
  • 当 nums 为空时 说明已经全部添加完成了 这时候将这个结果存入 结果数组中
  • 最后将这个结果数组进行返回即可。

原型图

image-20220126203754555

效果

源代码 ​

js
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function (nums) {
	if (nums.length === 1) {
		return [nums]
	}
	let res = []
	const diff = (path, parameter) => {
		if (parameter.length === 0) {
			res.push(path)
			return
		}
		for (let i = 0; i < parameter.length; i++) {
			let item = parameter[i]
			parameter.splice(i, 1)
			diff([...path, item], parameter)
			parameter.splice(i, 0, item)
		}
	}
	diff([], nums)
}
permute([1, 2, 3])
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function (nums) {
	if (nums.length === 1) {
		return [nums]
	}
	let res = []
	const diff = (path, parameter) => {
		if (parameter.length === 0) {
			res.push(path)
			return
		}
		for (let i = 0; i < parameter.length; i++) {
			let item = parameter[i]
			parameter.splice(i, 1)
			diff([...path, item], parameter)
			parameter.splice(i, 0, item)
		}
	}
	diff([], nums)
}
permute([1, 2, 3])

全排列 Ⅱ ​

考点

难度：中级

思想：回溯

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=851006005&bvid=BV1GL4y1x7RP&cid=494084751&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=851006005&bvid=BV1GL4y1x7RP&cid=494084751&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2] 输出： [[1,1,2], [1,2,1], [2,1,1]] 示例 2：

输入：nums = [1,2,3] 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

1 <= nums.length <= 8 -10 <= nums[i] <= 10

解题思路 ​

这题的解题思路和上一题是 全排列 是一样的，区别在于多了一个条件

  • 数组内容可能会有重复的数字

所以整体的逻辑和上一题基本保持一致，使用回溯的套路即可快速解题。因为数组的成员可能会重复，所以和上一题相比会多几步操作：

  1. 先将整个数组进行一次排序

  2. 我们我们分别创建两个数组 一个空数组 一个存放 nums

  3. 每次递归都往第一个数组中存放一个 nums 中的一个值 nums 就减去一个值

  4. 如果 nums 中取的值和前一个取的值一样，则直接跳过 取下一个值

  5. 递归不断执行上面那个过程的

  6. 当 nums 为空时 说明已经全部添加完成了 这时候将这个结果存入 结果数组中

  7. 最后将这个结果数组进行返回即可。

原型图

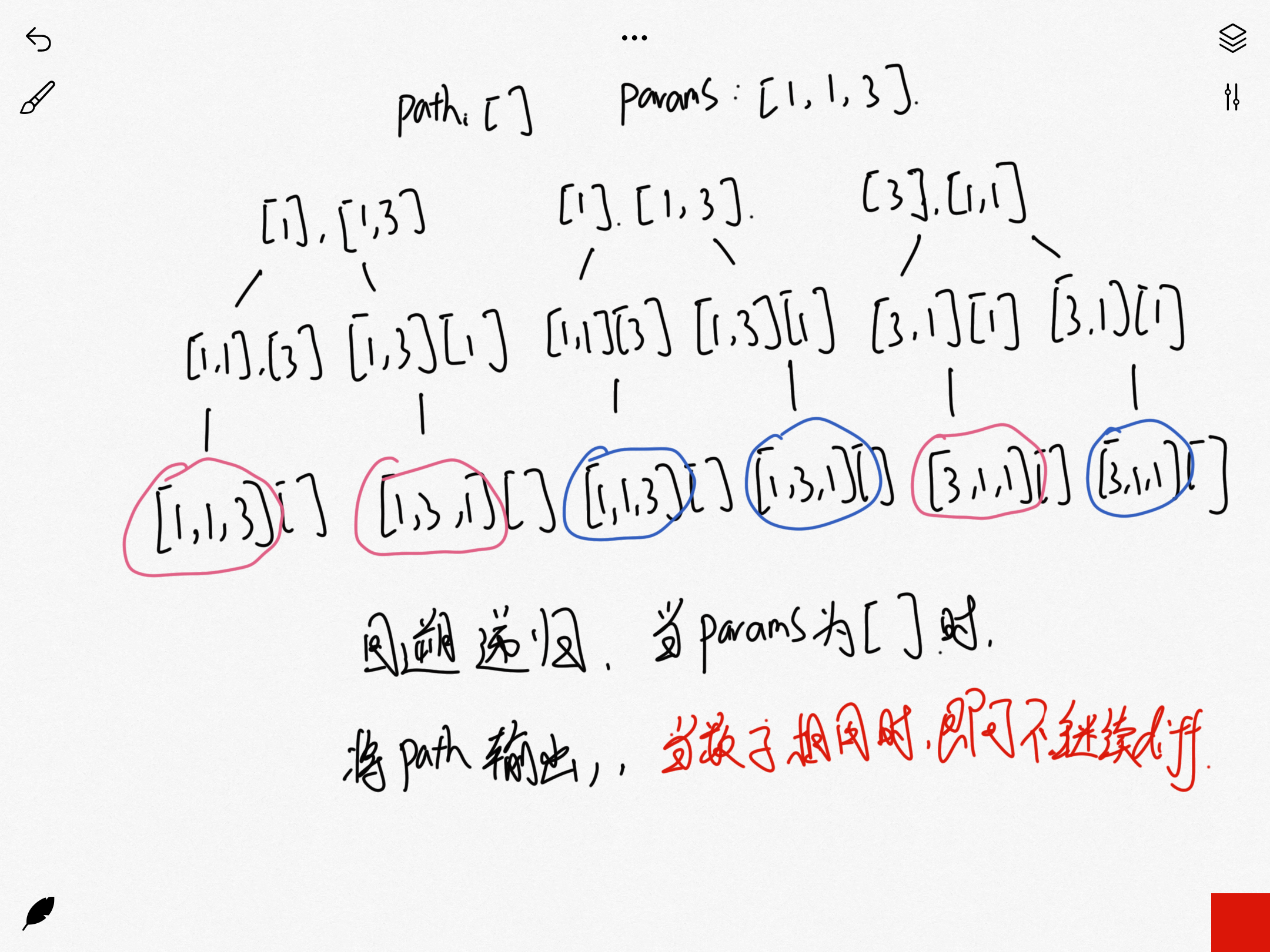
image-20220127212353493

效果

image-20220127212410423

源代码 ​

js
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permuteUnique = function (nums) {
	if (nums.length === 1) {
		return [nums]
	}
	nums.sort((a, b) => a - b)
	let res = []
	let temp = null
	const diff = (path, params) => {
		if (params.length === 0) {
			res.push(path)
			return
		}
		for (let i = 0; i < params.length; i++) {
			if (params[i] === params[i - 1]) {
				continue
			} else {
				temp = params[i]
				params.splice(i, 1)
				diff([...path, temp], params)
				params.splice(i, 0, temp)
			}
		}
	}
	diff([], nums)
	return res
}
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permuteUnique = function (nums) {
	if (nums.length === 1) {
		return [nums]
	}
	nums.sort((a, b) => a - b)
	let res = []
	let temp = null
	const diff = (path, params) => {
		if (params.length === 0) {
			res.push(path)
			return
		}
		for (let i = 0; i < params.length; i++) {
			if (params[i] === params[i - 1]) {
				continue
			} else {
				temp = params[i]
				params.splice(i, 1)
				diff([...path, temp], params)
				params.splice(i, 0, temp)
			}
		}
	}
	diff([], nums)
	return res
}

旋转图像 ​

考点

难度：中级

思想：交换、找规律

题目 ​

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出：[[7,4,1],[8,5,2],[9,6,3]] 示例 2：

输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

解题思路 ​

这题我首先想到的是 暴力破解法，只需要记录一下坐标，就能够非常快速的方式进行解题了!

但是题目是有要求的，要求我们只能原地的修改数组，所以暴力破解法在这里不能使用，得使用更加巧妙的方法。这个方法我是看官方解题的视频学来的。

将每个点都使用坐标进行表示，我们会发现 旋转 90 度其实是内部的坐标一些变化。如：

(0,0) => (2,0)
(2,0) => (2,2)
(2,2) => (0,2)
(0,2) => (0,0)
(0,0) => (2,0)
(2,0) => (2,2)
(2,2) => (0,2)
(0,2) => (0,0)

涉及到的不是两两交换，而是四个元素之间的互相交换。

所以真的难的是我们要判断哪四个点之间要交换，最后执行一次交换 就能进行解题了。 也推荐大家看下 leetcode 官方解题

原型图

效果

源代码 ​

js
// 暴力破解法
var rotate = function (matrix) {
	let res = []
	for (let i = 0; i < matrix.length; i++) {
		let temp = []
		for (let j = matrix.length - 1; j >= 0; j--) {
			temp.push(matrix[j][i])
		}
		res.push(temp)
	}
	matrix = res
}

// leetcode官方解题 - 四四交换
var rotate = function (matrix) {
	let n = matrix.length
	let temp
	for (let i = 0; i < n / 2; i++) {
		for (let j = i; j < n - 1 - i; j++) {
			// 这里是四个点进行互相交换
			temp = matrix[i][j]
			matrix[i][j] = matrix[n - 1 - j][i]
			matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j]
			matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i]
			matrix[j][n - 1 - i] = temp
		}
	}
	console.log(matrix)
}
// 暴力破解法
var rotate = function (matrix) {
	let res = []
	for (let i = 0; i < matrix.length; i++) {
		let temp = []
		for (let j = matrix.length - 1; j >= 0; j--) {
			temp.push(matrix[j][i])
		}
		res.push(temp)
	}
	matrix = res
}

// leetcode官方解题 - 四四交换
var rotate = function (matrix) {
	let n = matrix.length
	let temp
	for (let i = 0; i < n / 2; i++) {
		for (let j = i; j < n - 1 - i; j++) {
			// 这里是四个点进行互相交换
			temp = matrix[i][j]
			matrix[i][j] = matrix[n - 1 - j][i]
			matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j]
			matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i]
			matrix[j][n - 1 - i] = temp
		}
	}
	console.log(matrix)
}

字母异位词分组 ​

考点

难度：中级

思想：我没有想到什么优秀的方式解题，就正常的数据处理的方式解题

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=808604282&bvid=BV1j34y127cL&cid=497069690&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=808604282&bvid=BV1j34y127cL&cid=497069690&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。

字母异位词 是由重新排列源单词的字母得到的一个新单词，所有源单词中的字母通常恰好只用一次。

示例 1:

输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]

输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

示例 2:

输入: strs = [""]

输出: [[""]]

示例 3:

输入: strs = ["a"]

输出: [["a"]]
示例 1:

输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]

输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

示例 2:

输入: strs = [""]

输出: [[""]]

示例 3:

输入: strs = ["a"]

输出: [["a"]]

解题思路 ​

这题我没有找到什么比较优秀的思路思路解题，有点类似于是暴力解题了。

  • 一次 for 循环，遍历一整个数组

  • 初始化一个对象

  • 将每次遍历到的字符串进行一次排序，再转成字符串，以这个字符串作为 key

    • 判断对象中是否有这个为 key 的值，如果没有将这个 key 的值作为一个数组的方式存入

    • 如果有这个 key，则把遍历到的这个值插入到这个 key 的数组中

  • 遍历结束，通过 Object.values()将值以一个数组的形式返回

这个解题思路我在 leetcode 上速度能击败 93.96%的人，但是内存消耗比较大只能击败 5%的人。

此外这里还获得了另外一个收获，就是我们要给字符串数组排序直接使用sort()即可，刚开始我一直使用sort((a,b)=>a-b)这套一直不能成功。

原型图

image-20220129205008075

效果

结果

源代码 ​

js
/**
 * @param {string[]} strs
 * @return {string[][]}
 */
var groupAnagrams = function (strs) {
	let obj = {}
	for (let i = 0; i < strs.length; i++) {
		let tes = [...strs[i]].sort().join('')
		if (!obj[tes]) {
			obj[tes] = []
			obj[tes].push(strs[i])
		} else {
			obj[tes].push(strs[i])
		}
	}
}
/**
 * @param {string[]} strs
 * @return {string[][]}
 */
var groupAnagrams = function (strs) {
	let obj = {}
	for (let i = 0; i < strs.length; i++) {
		let tes = [...strs[i]].sort().join('')
		if (!obj[tes]) {
			obj[tes] = []
			obj[tes].push(strs[i])
		} else {
			obj[tes].push(strs[i])
		}
	}
}

Pow(x,n) ​

考点

难度：中级

思想：处理好特殊的边界条件，避免不必要的计算

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=978694244&bvid=BV1F44y1W7RB&cid=497803785&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=978694244&bvid=BV1F44y1W7RB&cid=497803785&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，xn ）。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000
示例 2：

输入：x = 2.10000, n = 3
输出：9.26100
示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25
示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000
示例 2：

输入：x = 2.10000, n = 3
输出：9.26100
示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

解题思路 ​

正常解题， 只是有几个边界条件需要去掉

当 n 为 0 时，直接输出 1 (任何数的 0 次方都等于 1)

  • 当 n 为负数时， x 为 1/x n 转为绝对值进行就算

当以上的两个条件筛除过后，我们再筛除 X 的情况

  • 当 x 为 1 时， 直接返回 1

  • 当 x 为-1 时，判断 n 的绝对值对 2 取余是否能整除 整除返回 1 不整除返回-1

不符合以上条件 正常处理即可

原型图

image-20220130190556503

效果

image-20220130190713035

源代码 ​

js
/**
 * @param {number} x
 * @param {number} n
 * @return {number}
 */
var myPow = function (x, n) {
	if (n === 0) {
		return 1
	}
	if (n < 0) {
		n = Math.abs(n)
		x = 1 / x
	}
	if (x === 1) {
		return 1
	}
	if (x === -1) {
		return Math.abs(n) % 2 === 0 ? 1 : -1
	}
	let res = x
	for (let i = 0; i < n - 1; i++) {
		res = res * x
		if (res === 0) {
			break
		}
	}
	return res
}
/**
 * @param {number} x
 * @param {number} n
 * @return {number}
 */
var myPow = function (x, n) {
	if (n === 0) {
		return 1
	}
	if (n < 0) {
		n = Math.abs(n)
		x = 1 / x
	}
	if (x === 1) {
		return 1
	}
	if (x === -1) {
		return Math.abs(n) % 2 === 0 ? 1 : -1
	}
	let res = x
	for (let i = 0; i < n - 1; i++) {
		res = res * x
		if (res === 0) {
			break
		}
	}
	return res
}

螺旋矩阵 ​

考点

难度：中级

思想：可以使用循环或递归解题

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=808635799&bvid=BV1W34y127h1&cid=498538290&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=808635799&bvid=BV1W34y127h1&cid=498538290&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]
示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

解题思路 ​

这题的思路是我们需要将每个点的坐标给记下来，然后记住每个点走动的位置的大小，用(i,j)记录当前的点，当我们每次

  • 右走 每次 i+0 j+1

  • 向下 每次 i+1 j+0

  • 向左 每次 i-1 j+0

  • 向上 每次 i+0 j-1

然后我们要做的是 顺时针是 不断 执行 右=>下=>左=>上 的过程 并把每次踩到的点都存入新的数组中，当走到边界时 换个位置 边界：

  • 当 i 或者 j 小于 0 （左边界）

  • 当 i 或者 j 等于边界时 （有边界）

  • 当 i 和 j 都访问到踩过的点时 换方向

原型图

image-20220131181817283

效果

image-20220131180308414

源代码 ​

js
/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
var spiralOrder = function (matrix) {
	let rowCount = matrix.length
	let colCount = matrix[0].length
	const position = [
		[0, 1],
		[1, 0],
		[0, -1],
		[-1, 0],
	]
	let directive = 0

	let res = []
	let row = 0,
		col = -1
	while (res.length < rowCount * colCount) {
		const nextRow = row + position[directive][0]
		const nextCol = col + position[directive][1]
		if (
			nextRow < 0 ||
			nextRow === rowCount ||
			nextCol < 0 ||
			nextCol === colCount ||
			matrix[nextRow][nextCol] === ''
		) {
			directive = (directive + 1) % position.length
			continue
		}
		res.push(matrix[nextRow][nextCol])
		matrix[nextRow][nextCol] = ''
		row = nextRow
		col = nextCol
	}
	return res
}
/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
var spiralOrder = function (matrix) {
	let rowCount = matrix.length
	let colCount = matrix[0].length
	const position = [
		[0, 1],
		[1, 0],
		[0, -1],
		[-1, 0],
	]
	let directive = 0

	let res = []
	let row = 0,
		col = -1
	while (res.length < rowCount * colCount) {
		const nextRow = row + position[directive][0]
		const nextCol = col + position[directive][1]
		if (
			nextRow < 0 ||
			nextRow === rowCount ||
			nextCol < 0 ||
			nextCol === colCount ||
			matrix[nextRow][nextCol] === ''
		) {
			directive = (directive + 1) % position.length
			continue
		}
		res.push(matrix[nextRow][nextCol])
		matrix[nextRow][nextCol] = ''
		row = nextRow
		col = nextCol
	}
	return res
}

跳跃游戏 ​

考点

难度：中级

思想：类似贪心算法、循环判断

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=636167573&bvid=BV1Fb4y1J7aS&cid=499086665&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=636167573&bvid=BV1Fb4y1J7aS&cid=499086665&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个下标。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。
示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

解题思路 ​

这题类似使用贪心算法，我们到数组的每一个点，判断这个点所能到达的最大的数组索引位置 遍历下来 只要这个最大能够到达的位置+1(+1 是因为索引从 0 开始) 是否 大于等于数组的长度

  • 如果满足，则说明能够到达
  • 如果不满足，则说明不能到达 除了这个条件，还有前置条件
  • 当我们最大到达的位置于当前遍历的索引一致的时候，如果这个点刚好等于 0 并且这时候最大能到达的位置+1 也小于数组长度 则直接停止遍历 直接返回 false 即可

原型图

image-20220201113819746

效果

image-20220201113746900

源代码 ​

js
/**
 * @param {number[]} nums
 * @return {boolean}
 */
var canJump = function (nums) {
	let nextIndex = 0
	for (let i = 0; i < nums.length - 1; i++) {
		nextIndex = Math.max(nums[i] + i, nextIndex)
		if (nextIndex === i && nums[i] === 0 && nextIndex < nums.length) {
			break
		}
	}
	return nextIndex + 1 >= nums.length
}
/**
 * @param {number[]} nums
 * @return {boolean}
 */
var canJump = function (nums) {
	let nextIndex = 0
	for (let i = 0; i < nums.length - 1; i++) {
		nextIndex = Math.max(nums[i] + i, nextIndex)
		if (nextIndex === i && nums[i] === 0 && nextIndex < nums.length) {
			break
		}
	}
	return nextIndex + 1 >= nums.length
}

合并区间 ​

考点

难度：中级

思想：巧解，找规律

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=296188533&bvid=BV1aF411H7Pv&cid=499781906&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=296188533&bvid=BV1aF411H7Pv&cid=499781906&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。
示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

解题思路 ​

这题我的第一想法觉得需要处理很多东西，写了很久，加了很多的判断，终于完成，就是下面性能差的一个版本，之所以要保留下来就是整个题目深刻的让我意识到了，不应该埋头苦做，而是应该巧解。

比如这题，我们需要的是先将这个二维数组排序(根据二维数组的开始项进行排序)，因为在这道题中 开始区间和结束区间，相对更加重要的一个是开始区间，所以要根据其排序：

  • 如果一个区间的开始区间就比要对比结束区间更大时，则两者肯定时不在一个区间了
  • 因为我们做过排序，所以现在遍历到的这个区间的开始区间一定是大于 要对比这个区间的开始区间的
  • 可以发现，因为排序 使得我们可以省略掉很多的 对比条件

如：未排序之前，我的性能差版本使用两层循环 耗时非常之久排序之后，性能更优版本只是用一层循环 极大加快了时间

原型图

image-20220202143415204

效果

image-20220202141628566

源代码 ​

js
/** 性能好
 * @param {number[][]} intervals
 * @return {number[][]}
 */
var merge = function (intervals) {
	if (intervals.length === 0 || intervals.length === 1) {
		return intervals
	}
	intervals.sort((a, b) => a[0] - b[0])
	let res = []
	let current = intervals[0]
	for (let i = 1; i < intervals.length; i++) {
		if (intervals[i][0] > current[1]) {
			res.push(current)
			current = intervals[i]
		} else {
			current[1] = Math.max(current[1], intervals[i][1])
		}
	}
	res.push(current)
}

/** 性能差
 * @param {number[][]} intervals
 * @return {number[][]}
 */
var merge = function (intervals) {
	let res = []
	for (let i = 0; i < intervals.length; i++) {
		if (res.length === 0) {
			res.push(intervals[i])
		} else {
			const [key, value] = intervals[i]
			handle(key, value)
		}
	}
	function handle(key, value) {
		for (let i = 0; i < res.length; i++) {
			const [pre, next] = res[i]
			if (key < pre && value >= pre) {
				res[i][0] = key
			} else if (key < pre && value < pre) {
				res.push([key, value])
			} else if (key > next) {
				if (i === res.length - 1) {
					res.push([key, value])
					break
				} else {
					continue
				}
			}
			if (value > next) {
				res[i][1] = value
			}
		}
	}
}
/** 性能好
 * @param {number[][]} intervals
 * @return {number[][]}
 */
var merge = function (intervals) {
	if (intervals.length === 0 || intervals.length === 1) {
		return intervals
	}
	intervals.sort((a, b) => a[0] - b[0])
	let res = []
	let current = intervals[0]
	for (let i = 1; i < intervals.length; i++) {
		if (intervals[i][0] > current[1]) {
			res.push(current)
			current = intervals[i]
		} else {
			current[1] = Math.max(current[1], intervals[i][1])
		}
	}
	res.push(current)
}

/** 性能差
 * @param {number[][]} intervals
 * @return {number[][]}
 */
var merge = function (intervals) {
	let res = []
	for (let i = 0; i < intervals.length; i++) {
		if (res.length === 0) {
			res.push(intervals[i])
		} else {
			const [key, value] = intervals[i]
			handle(key, value)
		}
	}
	function handle(key, value) {
		for (let i = 0; i < res.length; i++) {
			const [pre, next] = res[i]
			if (key < pre && value >= pre) {
				res[i][0] = key
			} else if (key < pre && value < pre) {
				res.push([key, value])
			} else if (key > next) {
				if (i === res.length - 1) {
					res.push([key, value])
					break
				} else {
					continue
				}
			}
			if (value > next) {
				res[i][1] = value
			}
		}
	}
}

插入区间 ​

考点

难度：中级

思想：巧解，找规律

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=893779070&bvid=BV1CP4y1A736&cid=500685063&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=893779070&bvid=BV1CP4y1A736&cid=500685063&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

给你一个 无重叠的 ，按照区间起始端点排序的区间列表。

在列表中插入一个新的区间，你需要确保列表中的区间仍然有序且不重叠（如果有必要的话，可以合并区间）。

示例 1：

输入：intervals = [[1,3],[6,9]], newInterval = [2,5]
输出：[[1,5],[6,9]]
示例 2：

输入：intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
输出：[[1,2],[3,10],[12,16]]
解释：这是因为新的区间 [4,8] 与 [3,5],[6,7],[8,10] 重叠。
示例 3：

输入：intervals = [], newInterval = [5,7]
输出：[[5,7]]
示例 4：

输入：intervals = [[1,5]], newInterval = [2,3]
输出：[[1,5]]
示例 5：

输入：intervals = [[1,5]], newInterval = [2,7]
输出：[[1,7]]
示例 1：

输入：intervals = [[1,3],[6,9]], newInterval = [2,5]
输出：[[1,5],[6,9]]
示例 2：

输入：intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
输出：[[1,2],[3,10],[12,16]]
解释：这是因为新的区间 [4,8] 与 [3,5],[6,7],[8,10] 重叠。
示例 3：

输入：intervals = [], newInterval = [5,7]
输出：[[5,7]]
示例 4：

输入：intervals = [[1,5]], newInterval = [2,3]
输出：[[1,5]]
示例 5：

输入：intervals = [[1,5]], newInterval = [2,7]
输出：[[1,7]]

解题思路 ​

这题这上一题的解题思路基本一致，只不过题目给我们的是一个不含重复的区间集合

再额外给我们一个区间，我们只要将这个额外的区间加入到区间集合中，这样这题就完全变成了上一题的解题思路

这题，我们需要的是先将这个二维数组排序(根据二维数组的开始项进行排序)，因为在这道题中 开始区间和结束区间，相对更加重要的一个是开始区间，所以要根据其排序：

  • 如果一个区间的开始区间就比要对比结束区间更大时，则两者肯定时不在一个区间了
  • 因为我们做过排序，所以现在遍历到的这个区间的开始区间一定是大于 要对比这个区间的开始区间的
  • 可以发现，因为排序 使得我们可以省略掉很多的 对比条件

如：未排序之前，我的性能差版本使用两层循环 耗时非常之久排序之后，性能更优版本只是用一层循环 极大加快了时间

原型图

image-20220203123043788

效果

image-20220203121650974

源代码 ​

js
/**
 * @param {number[][]} intervals
 * @param {number[]} newInterval
 * @return {number[][]}
 */
var insert = function (intervals, newInterval) {
	if (intervals.length === 0) {
		return [newInterval]
	}
	intervals.push(newInterval)
	intervals.sort((a, b) => a[0] - b[0])
	console.log(intervals)
	let res = []
	let current = intervals[0]
	for (let i = 1; i < intervals.length; i++) {
		if (intervals[i][0] > current[1]) {
			res.push(current)
			current = intervals[i]
		} else {
			current[1] = Math.max(current[1], intervals[i][1])
		}
	}
	res.push(current)
	return res
}
/**
 * @param {number[][]} intervals
 * @param {number[]} newInterval
 * @return {number[][]}
 */
var insert = function (intervals, newInterval) {
	if (intervals.length === 0) {
		return [newInterval]
	}
	intervals.push(newInterval)
	intervals.sort((a, b) => a[0] - b[0])
	console.log(intervals)
	let res = []
	let current = intervals[0]
	for (let i = 1; i < intervals.length; i++) {
		if (intervals[i][0] > current[1]) {
			res.push(current)
			current = intervals[i]
		} else {
			current[1] = Math.max(current[1], intervals[i][1])
		}
	}
	res.push(current)
	return res
}

螺旋矩阵 Ⅱ ​

考点

难度：中级

思想：巧解，找规律

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=296270518&bvid=BV1xF411J77W&cid=501071165&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=296270518&bvid=BV1xF411J77W&cid=501071165&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]
示例 2：

输入：n = 1
输出：[[1]]
示例 1：

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]
示例 2：

输入：n = 1
输出：[[1]]

解题思路 ​

这题是第 54 题相反过来的题。等于是告诉了我们螺旋输出的结果，需要让我们计算出原来的矩阵。思路和那一题是一样的，首先我们得先根据 n 初始化一个空的矩阵，并记录每个矩阵的坐标，当我们每次

  • 右走 每次 i+0 j+1

  • 向下 每次 i+1 j+0

  • 向左 每次 i-1 j+0

  • 向上 每次 i+0 j-1

然后我们要做的是 顺时针是 不断 执行 右=>下=>左=>上 的过程，并把每次踩到的点都存入新的数组中当走到边界时换个位置边界：

  • 当 i 或者 j 小于 0 （左边界）
  • 当 i 或者 j 等于边界时 （有边界）
  • 当 i 和 j 都访问到踩过的点时 换方向

每到一点时，将这个点存为上一次+1 的值，初始值为 1，最后再将原来的数组返回即可！

原型图

image-20220204131555110

效果

image-20220204113341407

源代码 ​

js
/**
 * @param {number} n
 * @return {number[][]}
 */
var generateMatrix = function (n) {
	let count = 1
	let arr = []
	for (let i = 0; i < n; i++) {
		arr.push([])
		for (let j = 0; j < n; j++) {
			arr[i][j] = 'xx'
		}
	}
	let rowCount = n,
		colCount = n
	const position = [
		[0, 1],
		[1, 0],
		[0, -1],
		[-1, 0],
	]
	let directive = 0

	let row = 0,
		col = -1
	let res = []
	while (res.length < rowCount * colCount) {
		const nextRow = row + position[directive][0]
		const nextCol = col + position[directive][1]
		if (
			nextRow < 0 ||
			nextRow === rowCount ||
			nextCol < 0 ||
			nextCol === colCount ||
			arr[nextRow][nextCol] !== 'xx'
		) {
			directive = (directive + 1) % position.length
			continue
		}
		res.push(arr[nextRow][nextCol])
		arr[nextRow][nextCol] = count++
		row = nextRow
		col = nextCol
	}
	return arr
}
/**
 * @param {number} n
 * @return {number[][]}
 */
var generateMatrix = function (n) {
	let count = 1
	let arr = []
	for (let i = 0; i < n; i++) {
		arr.push([])
		for (let j = 0; j < n; j++) {
			arr[i][j] = 'xx'
		}
	}
	let rowCount = n,
		colCount = n
	const position = [
		[0, 1],
		[1, 0],
		[0, -1],
		[-1, 0],
	]
	let directive = 0

	let row = 0,
		col = -1
	let res = []
	while (res.length < rowCount * colCount) {
		const nextRow = row + position[directive][0]
		const nextCol = col + position[directive][1]
		if (
			nextRow < 0 ||
			nextRow === rowCount ||
			nextCol < 0 ||
			nextCol === colCount ||
			arr[nextRow][nextCol] !== 'xx'
		) {
			directive = (directive + 1) % position.length
			continue
		}
		res.push(arr[nextRow][nextCol])
		arr[nextRow][nextCol] = count++
		row = nextRow
		col = nextCol
	}
	return arr
}

旋转链表 ​

考点

难度：中级

思想：链表、环形链表

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=338852619&bvid=BV1oR4y1j7SP&cid=501806082&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=338852619&bvid=BV1oR4y1j7SP&cid=501806082&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

给你一个链表的头节点 head ，旋转链表，将链表每个节点向右移动 k 个位置。

示例 1：

输入：head = [1,2,3,4,5], k = 2
输出：[4,5,1,2,3]
示例 2：

输入：head = [0,1,2], k = 4
输出：[2,0,1]
示例 1：

输入：head = [1,2,3,4,5], k = 2
输出：[4,5,1,2,3]
示例 2：

输入：head = [0,1,2], k = 4
输出：[2,0,1]

解题思路 ​

链表的题目对我来说算是非常恶心的题型，不是会做，而是不会写......*，*比如这题，思路出来了以后写了很久，最终还是参考了大神的解题思路才写出来

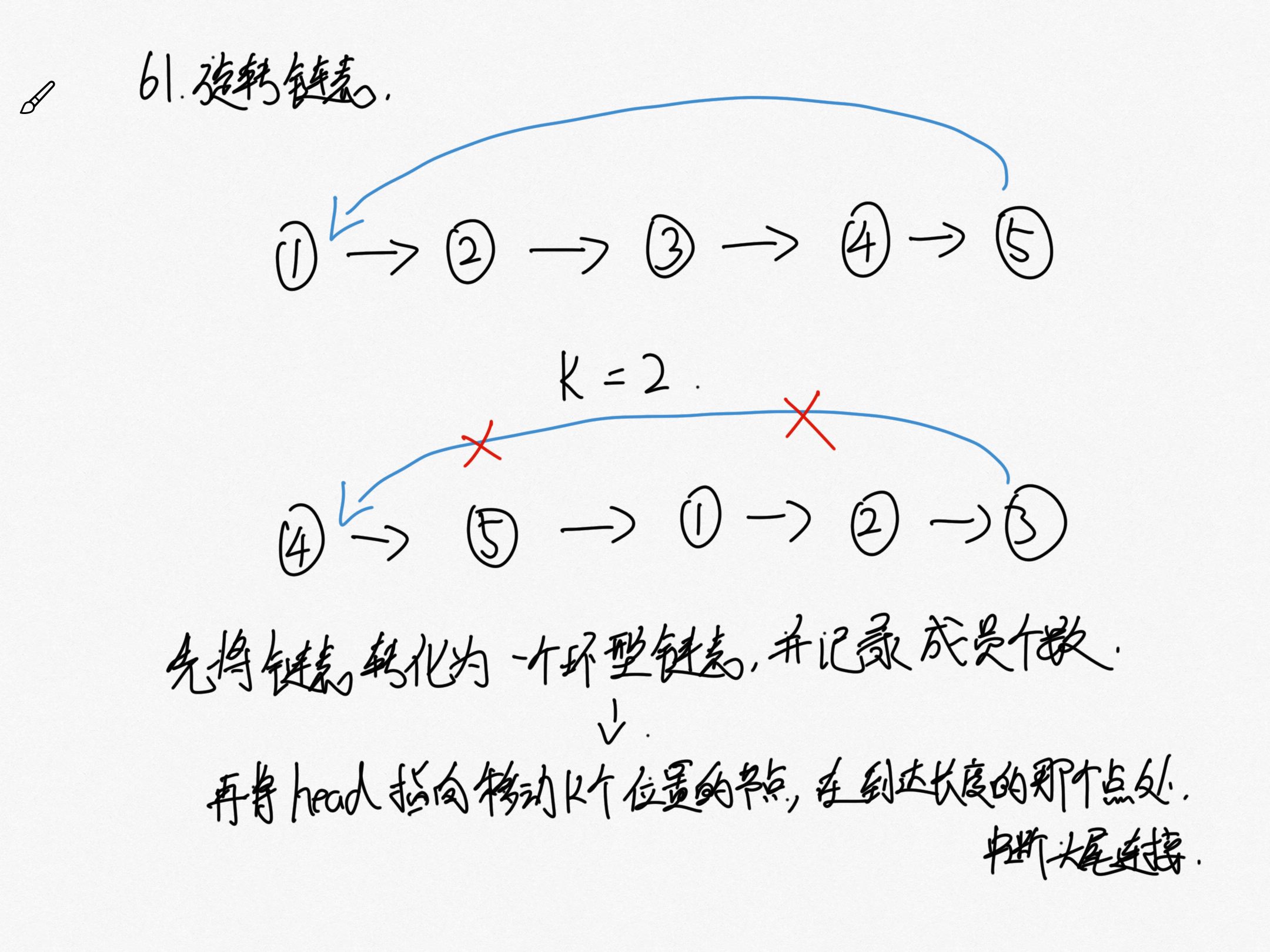
这题的思路也是相对比较清晰，先将这个链表的头尾进行链接，形成一个环形链表，

然后将移动 k 个位置的节点作为头节点，往后移动链表长度之后那个位置截断头尾的连接，

最后再将这个新的链表进行返回

原型图

image-20220205152134712

效果

image-20220205152107666

源代码 ​

js
/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @param {number} k
 * @return {ListNode}
 */
var rotateRight = function (head, k) {
	if (!head) {
		return null
	}
	let current = head
	let length = 0
	while (current) {
		length++
		if (!current.next) {
			current.next = head
			break
		}
		current = current.next
	}
	let temp = null
	let left = k % length
	while (left++ < length) {
		if (left === length) {
			temp = head
		}
		head = head.next
	}
	temp.next = null
	return head
}
/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @param {number} k
 * @return {ListNode}
 */
var rotateRight = function (head, k) {
	if (!head) {
		return null
	}
	let current = head
	let length = 0
	while (current) {
		length++
		if (!current.next) {
			current.next = head
			break
		}
		current = current.next
	}
	let temp = null
	let left = k % length
	while (left++ < length) {
		if (left === length) {
			temp = head
		}
		head = head.next
	}
	temp.next = null
	return head
}

不同路径 ​

考点

难度：中级

思想：动态规划、回溯

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=551310422&bvid=BV1ii4y1Z7Y7&cid=502717072&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=551310422&bvid=BV1ii4y1Z7Y7&cid=502717072&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=766337060&bvid=BV1Er4y1h7MW&cid=502721364&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=766337060&bvid=BV1Er4y1h7MW&cid=502721364&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7
输出：28
示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
   示例 3：

输入：m = 7, n = 3
输出：28
示例 4：

输入：m = 3, n = 3
输出：6
示例 1：

输入：m = 3, n = 7
输出：28
示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
   示例 3：

输入：m = 7, n = 3
输出：28
示例 4：

输入：m = 3, n = 3
输出：6

解题思路 ​

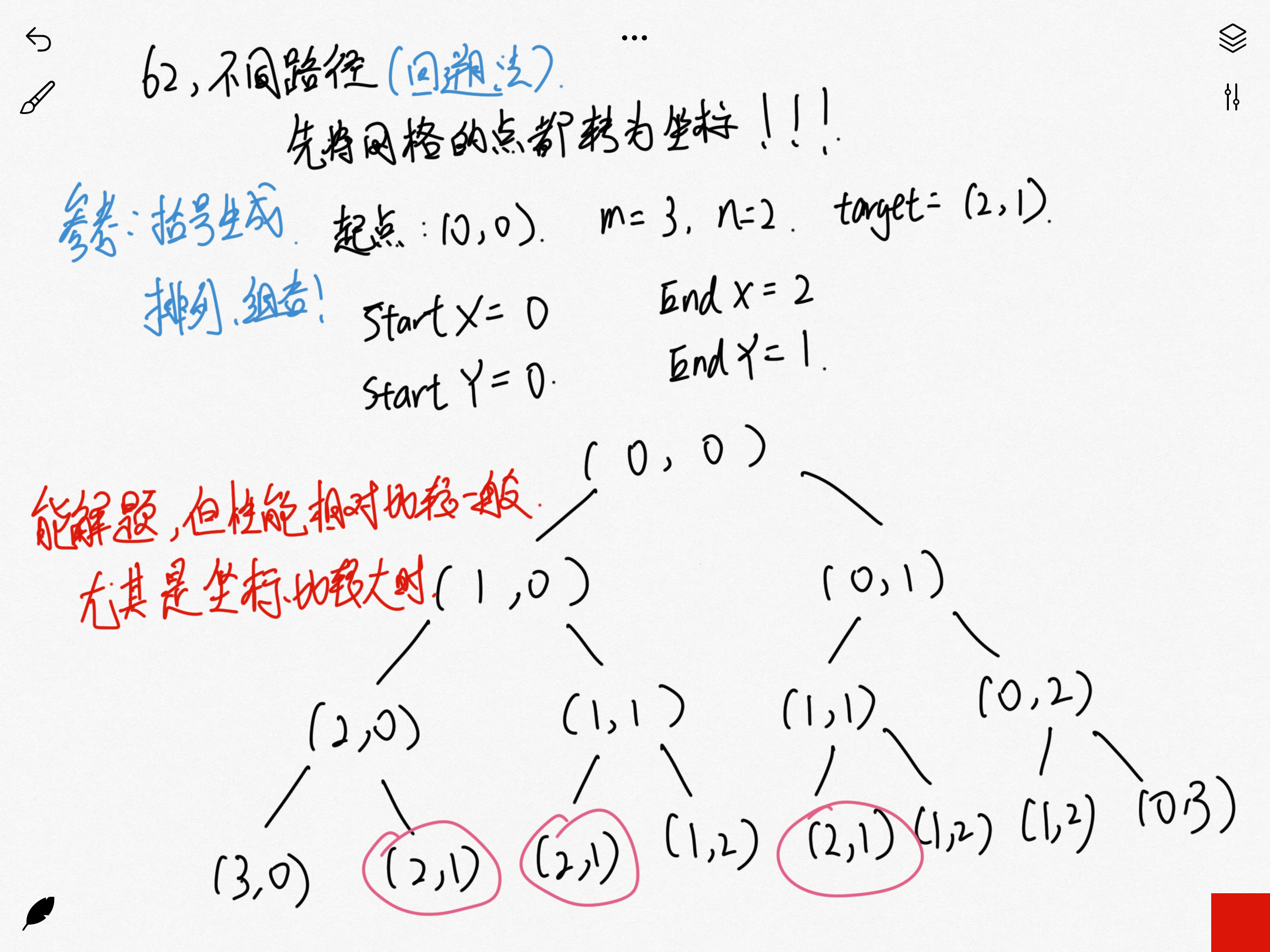
思路一：回溯递归的方式

这个方式的解题思路和补全括号的题目的思路是一样的，所以只要使用回溯的方式进行解题，那套熟悉的代码写下来很快就能解题，但是这样的解题效率是比较慢的，不是最优解

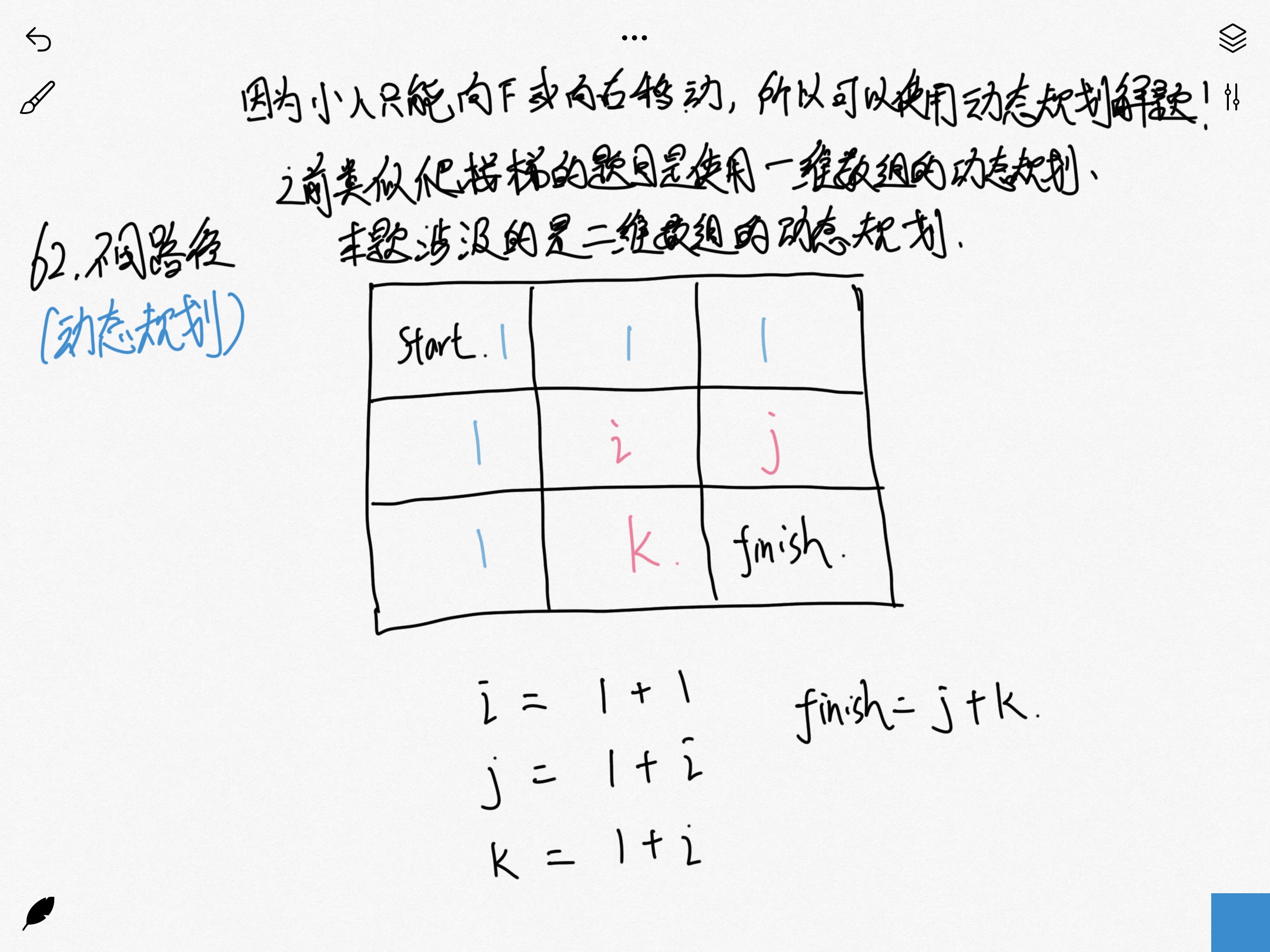
思路二：动态规划

之前处理的动态规划都是使用一维数组的，这回这个比较特殊是一个二维数组，其特点是 除了边界的点的走法都等于上面的路程+左边的路程，所以可以根据这个进行操作，最后输出指定点的值即可。

原型图

回溯法：

image-20220206194631662

动态规划：

image-20220206195346732

效果

image-20220206194600231

源代码 ​

js
/**
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
// 回溯法
var uniquePaths2 = function (m, n) {
	let startX = 0,
		startY = 0
	let endX = m - 1,
		endY = n - 1
	let res = 0
	const diff = (startX, startY) => {
		if (startX === endX && startY === endY) {
			res++
		}
		if (startY < endY) {
			diff(startX, startY + 1)
		}
		if (startX < endX) {
			diff(startX + 1, startY)
		}
	}
	diff(startX, startY)
	return res
}

// 动态规范
var uniquePaths = function (m, n) {
	const f = new Array(m).fill(1).map(() => new Array(n).fill(1))
	for (let i = 1; i < m; i++) {
		for (let j = 1; j < n; j++) {
			f[i][j] = f[i - 1][j] + f[i][j - 1]
		}
	}
	return f[m - 1][n - 1]
}
/**
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
// 回溯法
var uniquePaths2 = function (m, n) {
	let startX = 0,
		startY = 0
	let endX = m - 1,
		endY = n - 1
	let res = 0
	const diff = (startX, startY) => {
		if (startX === endX && startY === endY) {
			res++
		}
		if (startY < endY) {
			diff(startX, startY + 1)
		}
		if (startX < endX) {
			diff(startX + 1, startY)
		}
	}
	diff(startX, startY)
	return res
}

// 动态规范
var uniquePaths = function (m, n) {
	const f = new Array(m).fill(1).map(() => new Array(n).fill(1))
	for (let i = 1; i < m; i++) {
		for (let j = 1; j < n; j++) {
			f[i][j] = f[i - 1][j] + f[i][j - 1]
		}
	}
	return f[m - 1][n - 1]
}

不同路径 Ⅱ ​

考点

难度：中级

思想：动态规划

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=893797653&bvid=BV1SP4y1A7fG&cid=503160357&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=893797653&bvid=BV1SP4y1A7fG&cid=503160357&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：

1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1
示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：

1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

解题思路 ​

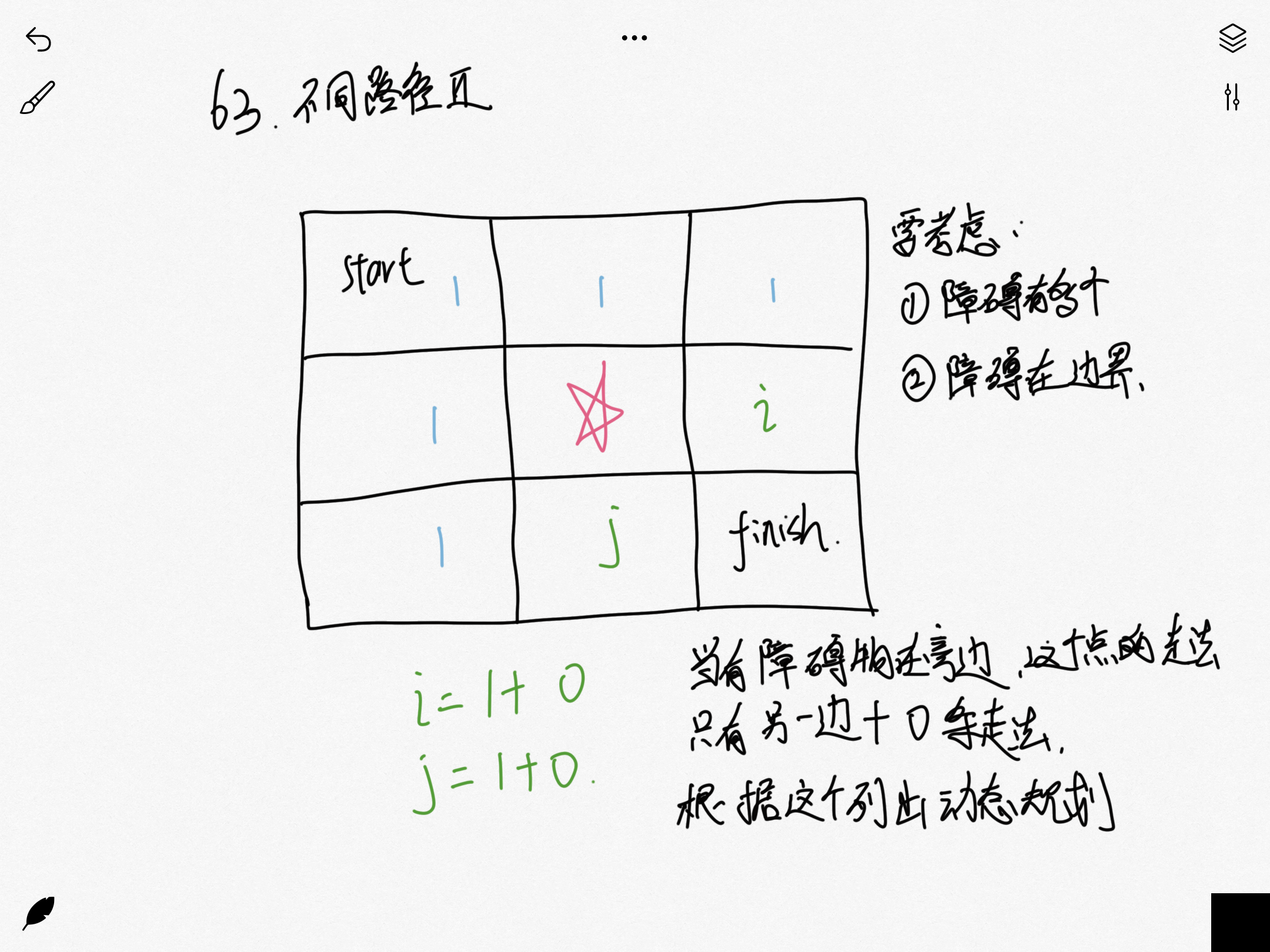
这题是 62 不同路径的升级版本，添加了障碍物的元素，更难了一点，但是任然可以使用动态规划进行解题。和上一题一个道理，因为机器人只能向右或者向下走，所以它到达一个点的走法等于左边格子走法+上面格子的走法，其次

  • 如果障碍物在左边，那它到达这个点的走法只等于到达上边的走法

  • 如果障碍物在目标点的上边，那它到达这个点的走法只等于到达左边的走法

以此可以列一个二维数组使用动态规划的方式进行求解

原型图

动态规划：

image-20220207124849691

效果

image-20220207113141867

源代码 ​

js
/**
 * @param {number[][]} obstacleGrid
 * @return {number}
 */
var uniquePathsWithObstacles = function (obstacleGrid) {
	let row = obstacleGrid.length
	let col = obstacleGrid[0].length
	for (let i = 0; i < row; i++) {
		for (let j = 0; j < col; j++) {
			if (obstacleGrid[i][j] === 1) {
				obstacleGrid[i][j] = -1
			}
		}
	}
	let xFlag = false
	let yFlag = false
	for (let i = 0; i < row; i++) {
		for (let j = 0; j < col; j++) {
			if (i === 0) {
				if (obstacleGrid[i][j] !== -1 && !xFlag) {
					obstacleGrid[i][j] = 1
				} else {
					xFlag = true
				}
			}
			if (j === 0) {
				if (obstacleGrid[i][j] !== -1 && !yFlag) {
					obstacleGrid[i][j] = 1
				} else {
					yFlag = true
				}
			}
		}
	}
	for (let i = 1; i < row; i++) {
		for (let j = 1; j < col; j++) {
			if (obstacleGrid[i][j] === -1) {
				continue
			} else if (obstacleGrid[i - 1][j] === -1) {
				obstacleGrid[i][j] = obstacleGrid[i][j - 1]
			} else if (obstacleGrid[i][j - 1] === -1) {
				obstacleGrid[i][j] = obstacleGrid[i - 1][j]
			} else {
				obstacleGrid[i][j] = obstacleGrid[i - 1][j] + obstacleGrid[i][j - 1]
			}
		}
	}
	return obstacleGrid[row - 1][col - 1] === -1
		? 0
		: obstacleGrid[row - 1][col - 1]
}
/**
 * @param {number[][]} obstacleGrid
 * @return {number}
 */
var uniquePathsWithObstacles = function (obstacleGrid) {
	let row = obstacleGrid.length
	let col = obstacleGrid[0].length
	for (let i = 0; i < row; i++) {
		for (let j = 0; j < col; j++) {
			if (obstacleGrid[i][j] === 1) {
				obstacleGrid[i][j] = -1
			}
		}
	}
	let xFlag = false
	let yFlag = false
	for (let i = 0; i < row; i++) {
		for (let j = 0; j < col; j++) {
			if (i === 0) {
				if (obstacleGrid[i][j] !== -1 && !xFlag) {
					obstacleGrid[i][j] = 1
				} else {
					xFlag = true
				}
			}
			if (j === 0) {
				if (obstacleGrid[i][j] !== -1 && !yFlag) {
					obstacleGrid[i][j] = 1
				} else {
					yFlag = true
				}
			}
		}
	}
	for (let i = 1; i < row; i++) {
		for (let j = 1; j < col; j++) {
			if (obstacleGrid[i][j] === -1) {
				continue
			} else if (obstacleGrid[i - 1][j] === -1) {
				obstacleGrid[i][j] = obstacleGrid[i][j - 1]
			} else if (obstacleGrid[i][j - 1] === -1) {
				obstacleGrid[i][j] = obstacleGrid[i - 1][j]
			} else {
				obstacleGrid[i][j] = obstacleGrid[i - 1][j] + obstacleGrid[i][j - 1]
			}
		}
	}
	return obstacleGrid[row - 1][col - 1] === -1
		? 0
		: obstacleGrid[row - 1][col - 1]
}

最小路径总和 ​

考点

难度：中级

思想：动态规划

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=636267723&bvid=BV1Ub4y1j7Gb&cid=503853839&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=636267723&bvid=BV1Ub4y1j7Gb&cid=503853839&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。
示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12
示例 1：

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。
示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

解题思路 ​

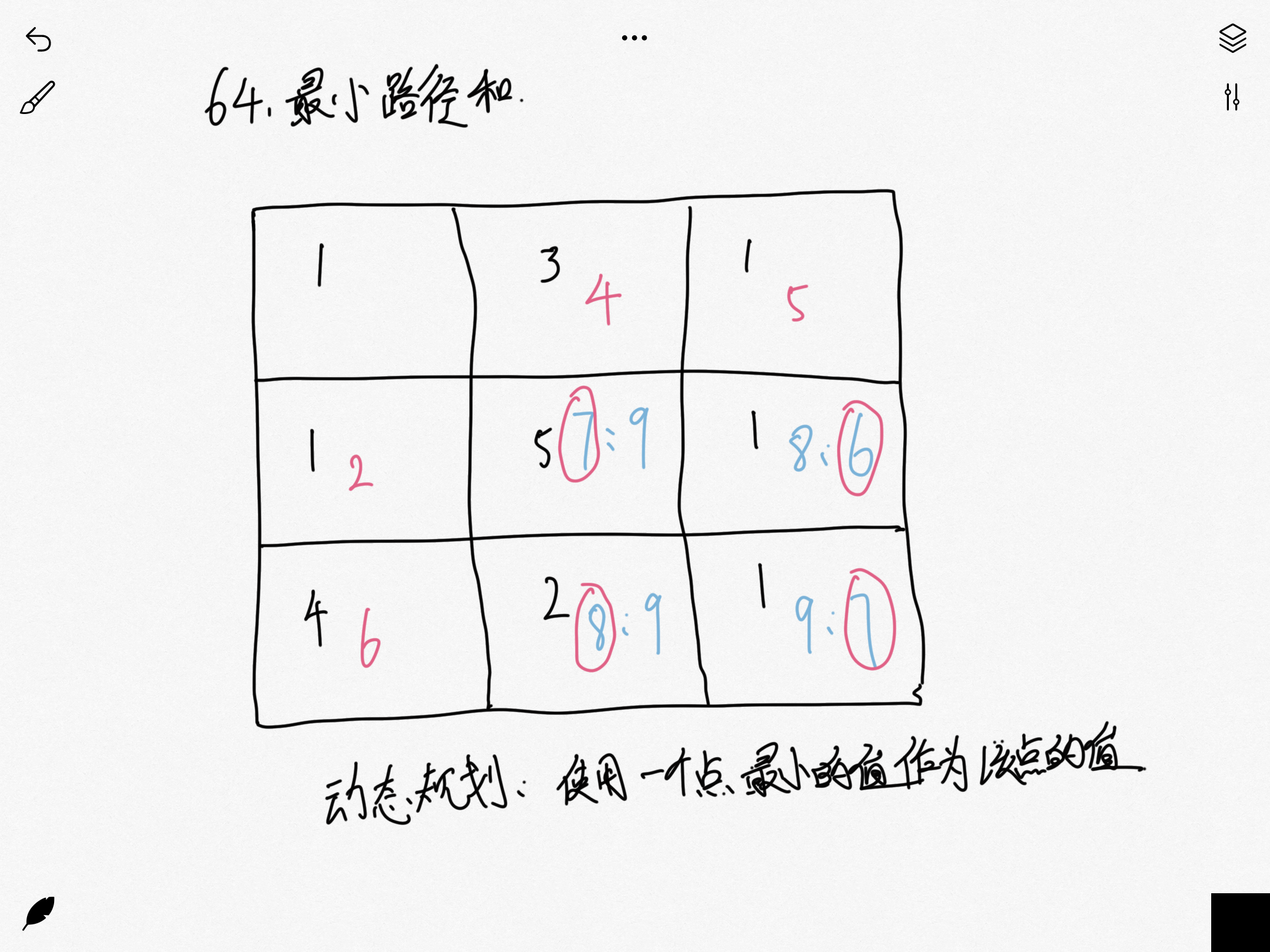
这题是前两题的升级版本，因为机器人只能向下和向右进行走，所以这题仍然是使用动态规划解题时最快的，到达一个点的值只只可能是：

上面点的值+当前值 或 左边的点值+当前值

我们取一个最小的值来取代当前的值即可，剩下的值就当填字游戏进行填即可。

原型图

image-20220208110456143

效果

image-20220208105400292

源代码 ​

js
/**
 * @param {number[][]} grid
 * @return {number}
 */
var minPathSum = function (grid) {
	let row = grid.length
	let col = grid[0].length
	for (let i = 0; i < row; i++) {
		for (let j = 0; j < col; j++) {
			if (i === 0) {
				grid[i][j] = (grid[i][j - 1] || 0) + grid[i][j]
			}
			if (j === 0) {
				grid[i][j] = (grid[i - 1] ? grid[i - 1][j] : 0) + grid[i][j]
			}
		}
	}

	for (let i = 1; i < row; i++) {
		for (let j = 1; j < col; j++) {
			grid[i][j] = Math.min(
				grid[i][j] + grid[i - 1][j],
				grid[i][j] + grid[i][j - 1]
			)
		}
	}
	return grid[row - 1][col - 1]
}
/**
 * @param {number[][]} grid
 * @return {number}
 */
var minPathSum = function (grid) {
	let row = grid.length
	let col = grid[0].length
	for (let i = 0; i < row; i++) {
		for (let j = 0; j < col; j++) {
			if (i === 0) {
				grid[i][j] = (grid[i][j - 1] || 0) + grid[i][j]
			}
			if (j === 0) {
				grid[i][j] = (grid[i - 1] ? grid[i - 1][j] : 0) + grid[i][j]
			}
		}
	}

	for (let i = 1; i < row; i++) {
		for (let j = 1; j < col; j++) {
			grid[i][j] = Math.min(
				grid[i][j] + grid[i - 1][j],
				grid[i][j] + grid[i][j - 1]
			)
		}
	}
	return grid[row - 1][col - 1]
}

二进制求和 ​

考点

难度：简单

思想：数组解题

:::demo

vue
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=381414179&bvid=BV1CZ4y1o734&cid=506952289&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>
<template>
	<div class="demo">
		<iframe
			src="//player.bilibili.com/player.html?aid=381414179&bvid=BV1CZ4y1o734&cid=506952289&page=1"
			scrolling="no"
			border="0"
			frameborder="no"
			framespacing="0"
			allowfullscreen="true"
		>
		</iframe>
	</div>
</template>
<style>
.demo > iframe {
	width: 100%;
	height: 450px;
}
</style>

:::

题目 ​

给你两个二进制字符串，返回它们的和（用二进制表示）。

输入为 非空 字符串且只包含数字 1 和 0。

示例 1:

输入: a = "11", b = "1"
输出: "100"
示例 2:

输入: a = "1010", b = "1011"
输出: "10101"
示例 1:

输入: a = "11", b = "1"
输出: "100"
示例 2:

输入: a = "1010", b = "1011"
输出: "10101"

解题思路 ​

这是一道难度为简单的题，我们之前做了十进制的加减，所以做这个二进制的简直就简单的不行了

我们需要知道的是，二进制相加时的进位 最多为 1

我们可以将整个整个字符串进行一次倒序，倒着计算，这样操作之后的结果我们再统一再进行一次反转

因为涉及到数组解题，这样操作添加的删除元素都在数组末尾，性能更高！

原型图

image-20220208110456143

效果

image-20220208105400292

源代码 ​

js
/**
 * @param {string} a
 * @param {string} b
 * @return {string}
 */
var addBinary = function (a, b) {
	let lengthdep = a.length - b.length
	if (lengthdep > 0) {
		b = '0'.repeat(lengthdep) + b
	} else if (lengthdep < 0) {
		a = '0'.repeat(Math.abs(lengthdep)) + a
	}
	a = [...a].reverse()
	b = [...b].reverse()
	let sum = []
	let add = 0
	for (let i = 0; i < a.length; i++) {
		let temp = Number(a[i]) + Number(b[i]) + add
		if (temp > 1) {
			sum[i] = temp % 2
			add = 1
		} else {
			sum[i] = temp
			add = 0
		}
	}
	if (add) {
		sum.push(add)
	}
	return sum.reverse().join('')
}
/**
 * @param {string} a
 * @param {string} b
 * @return {string}
 */
var addBinary = function (a, b) {
	let lengthdep = a.length - b.length
	if (lengthdep > 0) {
		b = '0'.repeat(lengthdep) + b
	} else if (lengthdep < 0) {
		a = '0'.repeat(Math.abs(lengthdep)) + a
	}
	a = [...a].reverse()
	b = [...b].reverse()
	let sum = []
	let add = 0
	for (let i = 0; i < a.length; i++) {
		let temp = Number(a[i]) + Number(b[i]) + add
		if (temp > 1) {
			sum[i] = temp % 2
			add = 1
		} else {
			sum[i] = temp
			add = 0
		}
	}
	if (add) {
		sum.push(add)
	}
	return sum.reverse().join('')
}

Excel表列名称 ​

考点

难度：简单

思想：进制转换、递归解题

题目 ​

给你一个整数 columnNumber ，返回它在 Excel 表中相对应的列名称。

例如：

A -> 1 B -> 2 C -> 3 ... Z -> 26 AA -> 27 AB -> 28 ...

输入：columnNumber = 1
输出："A"
示例 2：

输入：columnNumber = 28
输出："AB"
示例 3：

输入：columnNumber = 701
输出："ZY"
示例 4：

输入：columnNumber = 2147483647
输出："FXSHRXW"
输入：columnNumber = 1
输出："A"
示例 2：

输入：columnNumber = 28
输出："AB"
示例 3：

输入：columnNumber = 701
输出："ZY"
示例 4：

输入：columnNumber = 2147483647
输出："FXSHRXW"

解题思路 ​

这题采用的是递归的解题思路，本质上这题涉及的是进制转换问题，由我们所熟知的 10进制 => 26进制 所以我们可以类比我们熟知的 除二取余法 => 这里自然而然的编程 除26取余法

几个比较关键的边缘条件 还有要注意的是这里数字是从 1 开始 而不是我们所熟知的 10进制 从0开始

采用递归的方式就可以比较方便快速的解题了：

  • 不断的除以 26取余，当余数小于26时就用这个值当做index去取值即可

  • 当除以26的整数也大于26时，就将这个整数作为值再次执行一次上面的操作，直到得到小于26的整数时，作为index取值

  • 当除以26之后的值刚好为整数时，需要将这个值（-1），因为没有为0的索引，最小的索引是从1开始的，这个是唯一比较需要理解的点

    举例子：

    当值为52时:

    52/26 = 2，所以第一个索引值为2 第二个索引值为0（这是不对的，再这个题目里最小的是1，没有0），所以需要调整为：

    第一个值为1，第二个值为26 : AZ

效果

image-20220812212819815

源代码 ​

js
/**
 * @param {number} columnNumber
 * @return {string}
 */
var convertToTitle = function (columnNumber) {
	const map = {
		1: 'A',
		2: 'B',
		3: 'C',
		4: 'D',
		5: 'E',
		6: 'F',
		7: 'G',
		8: 'H',
		9: 'I',
		10: 'J',
		11: 'K',
		12: 'L',
		13: 'M',
		14: 'N',
		15: 'O',
		16: 'P',
		17: 'Q',
		18: 'R',
		19: 'S',
		20: 'T',
		21: 'U',
		22: 'V',
		23: 'W',
		24: 'X',
		25: 'Y',
		26: 'Z',
	}
	let str = ''
	const diff = num => {
		if (num <= 26) {
			str += map[num]
			return
		}
		let radix = num % 26 === 0 ? Math.floor(num / 26) - 1 : Math.floor(num / 26)
		if (radix > 26) {
			diff(radix)
		} else {
			str += map[radix]
		}
		diff(num - radix * 26)
	}
	diff(columnNumber)
	return str
}
/**
 * @param {number} columnNumber
 * @return {string}
 */
var convertToTitle = function (columnNumber) {
	const map = {
		1: 'A',
		2: 'B',
		3: 'C',
		4: 'D',
		5: 'E',
		6: 'F',
		7: 'G',
		8: 'H',
		9: 'I',
		10: 'J',
		11: 'K',
		12: 'L',
		13: 'M',
		14: 'N',
		15: 'O',
		16: 'P',
		17: 'Q',
		18: 'R',
		19: 'S',
		20: 'T',
		21: 'U',
		22: 'V',
		23: 'W',
		24: 'X',
		25: 'Y',
		26: 'Z',
	}
	let str = ''
	const diff = num => {
		if (num <= 26) {
			str += map[num]
			return
		}
		let radix = num % 26 === 0 ? Math.floor(num / 26) - 1 : Math.floor(num / 26)
		if (radix > 26) {
			diff(radix)
		} else {
			str += map[radix]
		}
		diff(num - radix * 26)
	}
	diff(columnNumber)
	return str
}

多数元素 ​

考点

难度：简单

思想：巧解

题目 ​

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1：

输入：nums = [3,2,3]
输出：3

示例 2：

输入：nums = [2,2,1,1,1,2,2]
输出：2
示例 1：

输入：nums = [3,2,3]
输出：3

示例 2：

输入：nums = [2,2,1,1,1,2,2]
输出：2

解题思路 ​

这题时间复杂度要求为O(n) 说明只能一层循环解题，这里借用了 数组 这么一数据结构进行解题（因为数组的下标index正好可以被我们用作key）

所以只要每遍历到一个数字，将数组这个索引下的值 +1 即可

当全部都执行结束之后，再次一层遍历，找出数组中哪个值大于 比对值， 那么那个值所对应的索引就是我们的答案！

效果

image-20220813210319911

源代码

js
/**
 * @param {number[]} nums
 * @return {number}
 */
var majorityElement = function (nums) {
	const arr = new Array(Math.max(...nums) + 1).fill(0)
	const check = nums.length / 2
	nums.forEach(num => {
		arr[num]++
	})
	let index = arr.findIndex((_, index) => {
		return arr[index] > check
	})
	return index
}
/**
 * @param {number[]} nums
 * @return {number}
 */
var majorityElement = function (nums) {
	const arr = new Array(Math.max(...nums) + 1).fill(0)
	const check = nums.length / 2
	nums.forEach(num => {
		arr[num]++
	})
	let index = arr.findIndex((_, index) => {
		return arr[index] > check
	})
	return index
}

Execl 表列序号 ​

考点

难度：简单

思想：进制转换、循环解题

题目 ​

给你一个字符串 columnTitle ，表示 Excel 表格中的列名称。返回 该列名称对应的列序号 。

例如：

A -> 1 B -> 2 C -> 3 ... Z -> 26 AA -> 27 AB -> 28 ...

示例 1:

输入: columnTitle = "A" 输出: 1 示例 2:

输入: columnTitle = "AB" 输出: 28 示例 3:

输入: columnTitle = "ZY" 输出: 701

解题思路 ​

这题是第 168题的 逆向解题思路，但是难度会比那题更低一点，也是使用进制转换的方法就可以快速解题了

先复习一下 二进制 => 十进制：

  • 1011 => 12(0次方)+12(1次方)+02(2次方)+12(3次方)

现在转换为我们题目的 26 进制

  • AZ => Z26(0次方)+A26(1次方) => 2626(0次方) + 126(1次方) => 52

所以按照下面的解题思路就可快速解题了！ --- 又水了一题

效果

image-20220813210827726

源代码

js
/**
 * @param {string} columnTitle
 * @return {number}
 */
var titleToNumber = function (columnTitle) {
	const map = {
		A: 1,
		B: 2,
		C: 3,
		D: 4,
		E: 5,
		F: 6,
		G: 7,
		H: 8,
		I: 9,
		J: 10,
		K: 11,
		L: 12,
		M: 13,
		N: 14,
		O: 15,
		P: 16,
		Q: 17,
		R: 18,
		S: 19,
		T: 20,
		U: 21,
		V: 22,
		W: 23,
		X: 24,
		Y: 25,
		Z: 26,
	}
	let count = 0
	for (let i = columnTitle.length - 1, j = 0; i >= 0; i--, j++) {
		count += map[columnTitle[i]] * Math.pow(26, j)
	}
	return count
}
/**
 * @param {string} columnTitle
 * @return {number}
 */
var titleToNumber = function (columnTitle) {
	const map = {
		A: 1,
		B: 2,
		C: 3,
		D: 4,
		E: 5,
		F: 6,
		G: 7,
		H: 8,
		I: 9,
		J: 10,
		K: 11,
		L: 12,
		M: 13,
		N: 14,
		O: 15,
		P: 16,
		Q: 17,
		R: 18,
		S: 19,
		T: 20,
		U: 21,
		V: 22,
		W: 23,
		X: 24,
		Y: 25,
		Z: 26,
	}
	let count = 0
	for (let i = columnTitle.length - 1, j = 0; i >= 0; i--, j++) {
		count += map[columnTitle[i]] * Math.pow(26, j)
	}
	return count
}